Вопросы по теории вероятностей + Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина.
X – случайная величина. x – значение случайной величины.
Дискретная случайная величина – можно пересчитать. Практически не возможное событие, вероятность которого близка к нулю 0 (0,01; 0,1). Практически достоверное событие, вероятность которого близка к единице 1 (0,99; 0,9888).
Сумма событий и произведение событий. А,В,….,G - события
Суммой событий
называется некоторое событие S=A+B+….+G=A
Пример: Допустим идет стрельба по мишени А 1 - попадание при первом выстреле А 2 - попадание при втором выстреле S=A 1 +A 2 (хотя бы одно попадание)
Произведением
некоторых событий называется событие, состоящее в совместном появлении всех этих событий. S=ABC…G=
Пример: А 1 - промах при первом выстреле А 2 - промах при втором выстреле А 3 - промах при третьем выстреле
Теорема сложения вероятностей. Вероятность двух не совместных событий равна сумме вероятностей этих событий. P(A) P(B) P(A+B)=P(A)+P(B) S=S 1 +S 2 +…+S n P(S)=P(S 1 )+P(S 2 )+…+P(S n ) Следствие: Если событие S 1 , S 2 , …, S n образуют полную группу не совместных событий, то сумма их вероятностей равна 1.
Противоположными событиями называются два не совместных события, образующие полную группу
.
Если два события A и B совместны, то вероятность совместного появления двух событий вычисляется по формуле:
Условие независимости события А от события В: P(A|B)=P(A), то P(B|A)=P(B)
Условие зависимости
события А от события В: P(A|B)
Вероятность произведения двух событий равна произведению вероятности одного из событий на условную вероятность другого, вычисленную при условии, что событие первое имело место: P(AB)=P(A)P(B|A), P(AB)=P(B)P(A|B) Следствие: Вероятность произведения нескольких не зависимых событий равна произведению вероятностей этих событий. P(A 1 A 2 …A n )=P(A 1 )P(A 2 )…P(A n ) Пример: на монете выпадет орел 2 раза S=A ор A ор S=P 2 (A)=(1/2) 2 =1/4
Закон распределения случайных величин Ряд и многоугольник распределений. Случайная величина - это величина, которая в результате опыта может принять то или иное значение не известное заранее какое. Большие буквы - случайные величины. Малые буквы - их возможные решения. Рассмотрим случайную дискретную величину Х с возможными значениями x 1 , x 2 , …, x n
В результате опыта :
Обозначим вероятность соответствующих событий через P i
Х полностью описана с вероятностной точки зрения, если мы зададим распределение вероятности p i (i=1,2…,n), то есть в точности указаны решения вероятности p i каждого события x i Этим будет установлен закон случайной величины x i . Законом распределения случайной величины называется всякое соотношение устанавливающее связь между возможными значениями случайных величин и соответствующими вероятностями. Простейшей формой записи законов распределения является таблица:
Многоугольник и ряд распределения полностью характеризует случайную величину и является одной из форм законов распределения. (Для непрерывной случайной величины построить невозможно).
Плотность и функция распределения. Функция распределения непрерывной случайной величины (Х), задана выражением:
F(4)=1 -> a4=1, a=0,25
Функция распределения Для непрерывной случайной величины Х вместо вероятности равенства Х=х используют вероятность Р(Х<х). F(x)=P(X<x) F-функция распределения случайной величины х F(x) -интегральный закон распределения или интегральная функция распределения. F(x) -самая универсальная характеристика случайной величины, она существует для всех случайных величин как дискретных так и непрерывных. Основные свойства функции распределения.
)=1
Для дискретной случайной величины:
Функция распределения любой дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которых происходят в точках соответствующих возможных значений случайных величин и равны вероятностям этих значений. Сумма всех скачков равна 1. F(x) непрерывной случайной величины
Часто используют величины квантиль
Квантиль - решение уравнения
Формула полной вероятности. Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий H 1 , H 2 , …, H n , образующие полную группу не совместных событий. Эти события назовем гипотезами. Докажем, что в этом случае вероятность событий:
Вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на условную вероятность события при этой гипотезе.
Теорема гипотез (формула Байеса). Пусть вероятность полной группы не совместных гипотез H 1 , H 2 , …, H n известны и равны P(H 1 ), P(H 2 ), …, P(H n ). Событие А может появиться совместно с условной вероятностью P(A|H i ) (i=1,2,…,n). Спрашивается, как следует изменить вероятности гипотез после проведения опытов в связи с появлением этого события. Иными словами, требуется найти условную вероятность P(H i ,A).
Формула Байеса:
Числовые характеристики случайных величин. 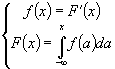
Закон распределения случайных величин, представленный в той или иной форме, дает исчерпывающее описание случайной величины. Наиболее существенные особенности распределения в компактной форме описываются так называемыми числовыми характеристиками случайных величин. Они играют в теории вероятности огромную роль, с их помощью облегчается решение вероятностных задач. Рассмотрим наиболее часто встречающиеся числовые характеристики. Характеристики положения. Мат. Ожидание Мода Медиана Важнейшая характеристика математическое ожидание , которая показывает среднее значение случайной величины. Математическое ожидание величины Х обозначается М[X], или m x . Для дискретных случайных величин математическое ожидание :
Сумма значений соответствующего значения на вероятность случайных величин.
Модой (Mod) случайной величины Х называют ее наиболее вероятное значение.Для дискретной случайной величины. Для непрерывной случайной величины.
Mod=X 3 Mod=X 0 Одно-модальное распределение
Много модальное распределение В общем случае Mod и математическое ожидание не совпадают.
Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один. Med разделяет площадь под кривой на 2 равные части. В случае одно-модального и симметричного распределения mx=Mod=Med
Моменты. Чаще всего на практике применяются моменты двух видов начальное и центральное.
Начальный момент.
Для непрерывной случайной величины Х начальным моментом
Пользуясь знаком (оператором) М, начальный момент
Центрированной случайной величиной соответственной случайной величины Х называют отклонение случайной величины Х от ее математического ожидания:
Для дискретных случайных величин имеем:
Моменты центрированной случайной величины носят название Центральных моментов
Центральный момент порядка
Для дискретных случайных величин:
Для непрерывных случайных величин:
Связь между центральными и начальными моментами различных порядков
Из всех моментов в качестве характеристики случайной величины чаще всего применяют первый момент (мат. ожидание)
Второй центральный момент называют дисперсией случайной величины. Он имеет обозначение:
Согласно определению
Для дискретной случайной величины:
Для непрерывной случайной величины:
Дисперсия случайной величины есть характеристика рассеянности (разбросанности) случайных величин Х около ее математического ожидания. Дисперсия означает рассеивание. Дисперсия имеет размерность квадрата случайной величины. Для наглядной характеристики рассеивания удобнее использовать величину, m y той, что и размерность случайной величины. С этой целью из дисперсии извлекают корень и получают величину, называемую - среднеквадратичным отклонением (СКО) случайной величины Х, при этом вводят обозначение:
Среднеквадратичное отклонение иногда называют "стандартом" случайной величины Х.
Итак:
Математическое ожидание m
x
и D
x
(или СКО
Равномерное распределение Равномерная плотность распределения определяется следующим образом:
Функция распределения определяется:
Найдем числовые характеристики:
Закон распределения Пуасона Рассмотрим дискретную случайную величину х, имеющую ряд распределения:
(k=m-1)
Нормальный закон распределения (закон Гауса) Главная особенность в том, что он является предельным законом, к которому приближаются другие распределения, при весьма часто встречающихся типичных условиях. Нормальный закон распределения характеризуется плотностью вероятности вида:
Можно показать, что дисперсия
Независимые случайные величины.
Случайные величины
x
и
y
независимы если вероятность
Для зависимых величин
x
и
y
вероятность
Корреляционным моментом или Ковариацией случайных величин x и y называют величину:
Можно показать, что для независимых случайных величин cov(x,y)=0
Коэффициент корреляций
Случайные величины x
1
, x
2
, x
3
, …, x
n
, называются не коррелированными, если
Теорема о числовых характеристиках
В общем случае:
Для не корреляционных случайных величин:
В широком смысле слова, закон больших чисел характеризует устойчивость средних. При очень большом числе случайных явлений - перестает быть случайным и может быть предсказан с большей степенью определенности. В узком смысле под законом больших чисел понимается ряд математических теорем, в которых устанавливаются факты приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Другая группа предельных теорем касается уже не предельных значений случайных величин, а предельных законов распределения. Эта группа теорем известна под названием " центральной предельной теоремы ". Неравенство Чебышева. P( |X-m x | > E) <= D x /E 2
Теорема Чебышева Теорема Чебышева дает одну из наиболее возможных форм закона больших чисел. Она устанавливает связь между средним арифметическим и ее математическим ожиданием наблюденных значений случайной величины.
Y
n
=( X
1
+ X
2
+ …. + X
n
) * 1/n = 1/n
M[Yn] = i/n
Мат ожидание среднего не зависит от n
Теорема Чебышева устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Теорема Чебышева: При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности n т ее математическому ожиданию. В можематической форме это означает следующее:
Теорема Бернулли Теорема Бернулли: При неограниченном увеличении числа опытов n , частота события a сходится по вероятности к его вероятности P
Центральная предельная теорема Рассмотрим одну из наиболее общих форм центральной предельной теоремы: Пусть имеется взвешенная сумма независимых случайных непрерывных величин x 1 , x 2 , x 3 , …., x n с произвольными законами распределения:
Пусть i-ая случайная величина имеет
Согласно теореме о числовых характеристиках случайных величин, получим:
Центральная предельная теорема утверждает, что при достаточно общих условиях распределения суммарной Y
n
при
Опыт показывает, что когда
Доверительный интервал и доверительная вероятность используется в математической статистике точности и надежности полученной оценки a* неизвестного параметра a.
Найдем значение интервала
вероятность, что выйдет за пределы интервала:
Интервал,
Вероятность
Оценка a* называется точечной оценкой.
Оценка
Рассмотрим серию из n однородных, не зависимых опытов, проводимых в одинаковых условиях, в каждом из которых может появиться или не появиться событие А . Вероятность появления F=P, не появления q=1-P. Предполагается, что вероятность р остается одной и той же в каждом опыте. Требуется найти вероятность Р m,n того, что А в этих n опытах появится ровно m раз (0<=m<=n).
Если производится n неизвестных опытов в каждом из которых событие А появляется с вероятностью Р , то вероятность того что событие А появится ровно m раз выражается формулой:
Задача на схему случаев В урне 3 белых и 4 черных шара. Какова вероятность изъятия из урны трех черных шаров? n - общее число возможных случаев изъятия 3 шаров из урны. m - число благоприятных случаев. (все три шара черные)
Задача на не совместные события. Мишень состоит из 2-х зон, при одном выстреле вероятность попадания в зону 1=0,2, в зону 2=0,4 Найти вероятность промаха?
А=А 1 +А 2 ; P(A)=P(A 1 )+P(A 2 )-P(A 1 A 2 ); P(A 1 A 2 )=0
Задача на умножение вероятностей. В урне находится 3 белых и 2 черных шара. Вынимается по 2 шара. Найти вероятность того, что оба шара белые? А 1 - первый шар белый. А 2 - второй шар белый. А=А 1 А 2
Задача на умножение вероятностей. В урне находятся 3 белых и 2 черных шара. Вынимают по очереди 2 шара, причем первый обратно возвращают. Какова вероятность что будут вынуты оба черных шара?
Задача на формулу полной вероятности. Имеется 3 урны. В одной 2 белых и 1 черный шар Во второй 1 белый и 1 черный шар. В третьей 3 белых и 2 черных шара. Выбирается одна из урн и из нее 1 шар. Какова вероятность, что шар черный? А - черный шар. P(A)=?
n=10 m=4
Второй способ через формулу полной вероятности. H 1 ; H 2 ; H 3 ;
Задача на теорему о повторении опытов. Проводят 4 независимых опыта. Вероятность события в каждом из опыте равна 0,3 Построить ряд и многогранник числа событий. Введем Х-число появлений событий в результате проведенных опытов. X=X 0 =0 X=X 1 =1 X=X 2 =2 X=X 3 =3 X=X 4 =4
P0,4=1*1*0,7 4 =0,0024
P1,4=
P2,4=
P3,4=
P4,4=
Задача на подсчет вероятностей Мишень состоит из 4 зон, производится один выстрел. Найти вероятность промоха, если вероятность попадание в зоны известна и равна: P 1 =0,1 P 2 =0,15 P 3 =0,20 P 4 =0,25 A - попадание в мишень.
Задача на условную вероятность. В урне находятся 3 белых и 2 черных шара. Вынимаются 2 шара. Найти вероятность, что оба шара белые. А 1 - белый шар А 2 - белый шар P(A 1 A 2 )=? C=A 1 A 2
Если первый шар возвращается в урну. P(A 1 )=P(A 2 )
a=? F(x)=? m
x
=?
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
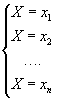
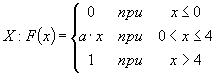
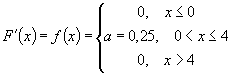
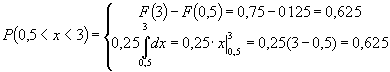 - два способа решения.
- два способа решения.
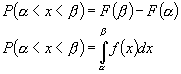
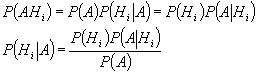
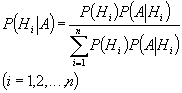
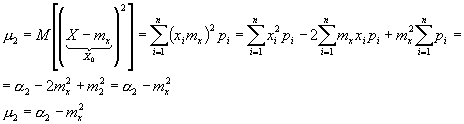
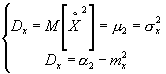
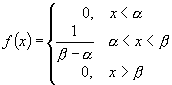
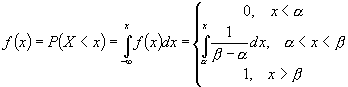
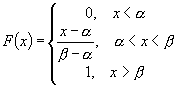
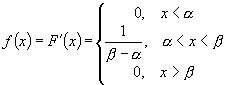
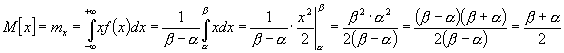
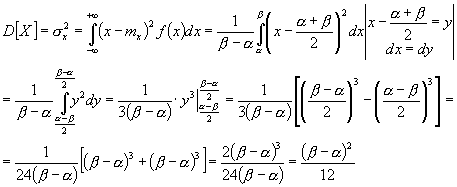
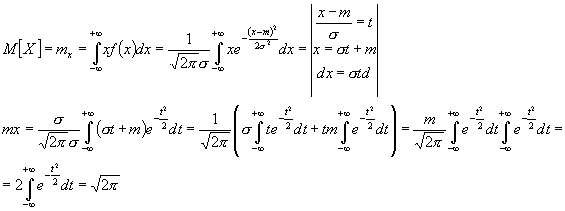
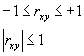
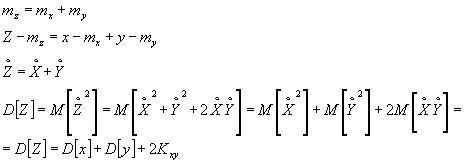
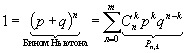 , где
, где
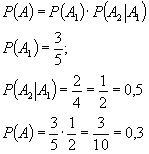
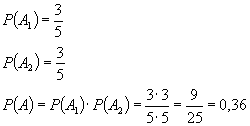
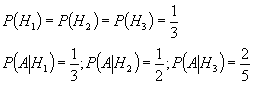
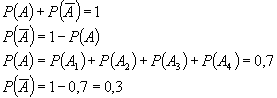
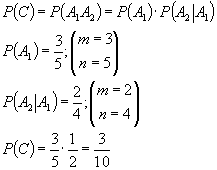
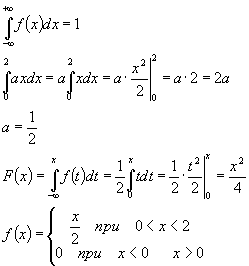
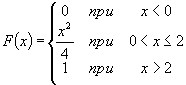
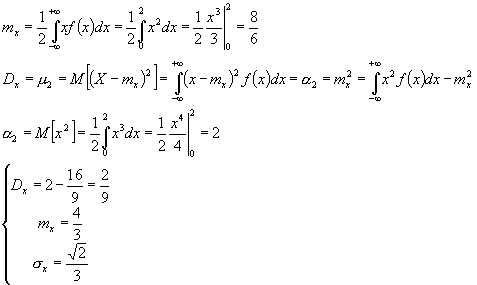
 Главная
Главная