Исследование наилучших приближений непрерывных периодических функций тригонометрическими тригонометрическими полиномами
Оглавление.
Введение Дипломная работа посвящена исследованию наилучших приближений непрерывных периодических функций тригонометрическими полиномами. В ней даются необходимые и достаточные условия для того, чтобы наилучшие приближения имели заданный (степенной) порядок убывания. Дипломная работа носит реферативный характер и состоит из “Введения” и восьми параграфов. В настоящей работе мы рассматриваем следующие задачи:
Подстановка u=cos(x) сводит задачу 1 к задаче 2. Достаточно, следовательно, рассматривать лишь задачу 2. Мы ограничимся случаем, когда j ( d ) О N a , для некоторого a , где j ( d ) - функция сравнения р-го порядка и для 0< d < h Ј p
С.Н.Бернштейн, Д.Джексон и Ш.Валле-Пуссен получили зависимости между оценками сверху для E n [ f ] и дифференциальными свойствами f . Некоторые дополнения к их теоремам доказаны А.Зигмундом. нам предстоит, поэтому, получить зависимости между дифференциальными свойствами f и оценками E n [ f ] снизу. Впервые задачами типа 1 занимался С.Н.Бернштейн. А именно, им получено ассимптотическое равенство:
где m - некоторое число. Наша основная теорема формулируется следующим образом: Пусть j О N a . Для того чтобы
необходимо, чтобы для любого натурального k> a , и достаточно, чтобы для некоторого натурального k> a
где
Изложим теперь кратко содержание каждого из параграфов работы. В § 1 даётся ряд вспомогательных определений, которые понадобятся в дальнейшей работе. В § 2 выводятся основные свойства модулей непрерывности высших порядков. Почти все эти свойства используются в дальнейшем тексте. § 3 посвящен обобщению теоремы Джексона. Как известно, Джексон доказал следующую теорему: если f имеет непрерывную r-ую производную f (r) , то
Таким образом, теорема Джексона дает оценку сверху для наилучших приближений, если известны дифференциальные свойства аппроксимируемой функции. В 1947 г. появилась работа С.Н.Бернштейна [1]. Одна из теорем этой работы содержит в качестве следствия такое предложение: пусть
Тогда
В § 3 доказываем:
В § 4 формулируется доказанное в работе С.Б.Стечкина [2] обобщение известного неравенства С.Н.Бернштейна [3], [4] для производных от тригонометрического полинома. Мы приводим затем ряд следствий из нашего неравенства (*). Они играют существенную роль при доказательстве теорем § 5. В § 5 рассматривается следующая задача. Пусть тригонометрический полином t n , близок в равномерной метрике к заданной функции f или последовательность полиномов { t n } достаточно хорошо аппроксимирует заданную функцию f . Как связаны тогда дифференциальные свойства f с дифференциальными свойствами t n ?
Если
t
n
, образуется из
f
посредством регулярного метода суммирования рядов Фурье, то ответ тривиален: для того чтобы
Оказывается, что этот результат сохраняется и для полиномов наилучшего приближения: для того, чтобы
Отметим еще один результат параграфа: для того чтобы
§ 6 посвящён “обратным теоремам” теории приближения. Известно предложение: пусть
Тогда, если
a
не целое,
r=
[
a
],
b
=
a
-
r
, то
f
имеет нерперывную производную
Случай целого a рассмотрен Зигмундом. В этом случае
Нетрудно показать, что эти два предложения эквивалентны следующему: пусть 0< a < k и
Тогда
В работе [3] С.Н.Бернштейн доказал также эквивалентность условий
Мы переносим эти теоремы на условия вида
где j О N a . Кроме того, в этом параграфе доказано, например, такое предложение: пусть k - натуральное число и
для того, чтобы
В конце параграфа даются уточнения теорем Валле-Пуссена. В § 7 доказывается основная теорема. Мы даём здесь же оценку E n [ f ] снизу, если
Именно, тогда
Случай a =0 установлен С.Н.Бернштейном [3].В § 8 мы рассматриваем несколько решений задач с использованием различных модулей непрерывности. § 1. Некоторые вспомогательные определения.
В работе рассматриваются непрерывные функции
f
с периодом 2
p
и их приближение тригонометрическими полиномами. Через
t
n
(
x
)
обозначается тригонометрический полином порядка не выше
n
, а через
t
n
*
(
x
)
=t
n
*
(
x,f
)-тригонометрический полином, наименее уклоняющийся от
f
среди всех
t
n
(x)
. Мы полагаем
Введём ряд определений.
Определение 1.
При каждом фиксированном
где С 8 -какая-нибудь положительная постоянная, которая не зависит от d и которая, вообще говоря, является различной для разных функций. Этот класс обозначается H a или Lip a.Определение 2. Обозначим при фиксированном натуральном r через W (r) L класс функций f , которая имеет абсолютно непрерывные производные до ( r- 1) порядка и у которой r -я производная принадлежит классу L . Определение 3. Для непрерывной на [ a,b ] функции f ( x ) назовём модулем непрерывности первого порядка или же просто модулем непрерывности функцию w ( d ) =w ( f; d ) , определённую на [ 0, b-a ] при помощи следующего равенства:
или, что то же самое,
Свойства модуля непрерывности :
Доказательство. Свойство 1) вытекает из определения модуля непрерывности.
Свойство 2) вытекает из того, что при больших d нам приходится рассматривать sup на более широком множестве значений h . Свойство 4) следует из того, что если мы число
Из неравенства (1.2) вытекает, что если
Теперь докажем свойство 3). Так как функция
f
(
x
) равномерно непрерывна на [
a,b
], то
а это и означает, что функция w(d) непрерывна.
Определение 4.
Пусть функция
f
(
x
)
определена на сегменте [
a,b
]
.
Тогда для любого натурального
k
и любых
а при
Лемма 1. При любых натуральных j и k справедливо равенство
Доказательство. Действительно, так как при любом натуральном k
то
Лемма доказана. Лемма 2. При любых натуральных k и n верна формула:
Доказательство. Воспользуемся индукцией по k . При k= 1 тождество (1.6) проверяется непосредственно:
Предполагая его справедливость при k- 1 ( k і 2), получим
Лемма доказана. Определение 5. Если измеримая периода ( b-a ) функция f ( x ) О L q ( L q -класс всех вещественных измеримых на [ a,b ] функции f ( x )), то под её интегральным модулем гладкости порядка k і 1 понимают функцию
Лемма 3. Если
Доказательство. В самом деле,
и так далее. Лемма доказана. Определение 6. Если функция f(x) ограничена на [ a,b ], то под её модулем гладкости порядка k і 1 понимают функцию
заданную для неотрицательных значений
Свойства модулей гладкости:
а при любом
5) Если функция
f
(
x
)
имеет всюду на [
a,b
] непрерывные производные до (
r-
1)-го порядка, и при этом (
r-1
)-я производная
Доказательство. 1) Свойство 1) немедленно вытекает из того, что
2) Свойство 2) доказывается точно так же, как и для случая обычного модуля непрерывности. 3) Предполагая для определённости, что d>d ’ , получим
Этим непрерывность функции w k ( d ) доказана.4) Используя равенство лемму 2 § 1, имеем
5) Используя равенства лемму 1 и лемму 3 § 1, получим
Определение 7. Пусть k -натуральное число. Будем говорить, что функция
где
Среди модулей непрерывности всех порядков особенно важное значение имеют случаи
k=
1 и
k=
2. Случай
k=
1 является классическим; вместо
Определение 8.
Зададим натуральное число
k.
Будем говорить, что функция
Нетрудно показать, что если
f
є
0, то
Определение 9.
Зафиксируем натуральное число
k
и функцию сравнения
k
-го порядка
Вместо
Если для последовательности функций { f n } (n=1,2,...)
где
С
10
не зависит от
n
, то будем писать:
Понятие классов
Определение 10. Зафиксируем число a >0 и обозначим через p наименьшее натуральное число, не меньше чем a ( p=- [- a ]). Будем говорить, что функция1) есть функция сравнения p -го порядка и
2) удовлетворяет условию: существует константа
С
11
>0 такая, что для
Условие 2) является небольшим ослаблением условия “
Определение 11.
Будем говорить, что функция
При выполнении этих условий будем писать
Определение 12. Ядром Дирихле n -го порядка называется функция
Это ядро является тригонометрическим полиномом порядка n и при этом
Определение 13. Ядром Фейера n -го порядка называется функция
Ядро Фейера F n ( t ) является средним арифметическим первых n ядер Дирихле, и значит, является тригонометрическим полиномом порядка ( n-1 ). Так что имеют место равенства
где D k ( t )-ядра Дирихле. Определение 14. Ядром Джексона n -го порядка называется функция
Свойства ядер Джексона. а) При каждом n ядро J n ( t ) является чётным неотрицательным тригонометрическим полиномом порядка 2 n -2 вида
где j k =j k ( n ) - некоторые числа
б)
в)
г)
Доказательство. а) Учитывая, что для ядер F n ( t ) Фейера имеют место равенства
где j k ( k =1,2,...,2 n -2) -некоторые числа, и в частности, в силу ортогональности тригонометрической системы функций найдем
Этим свойство а) доказано. б) Это равенство следует из равенства, полученного для j 0 .
в) Так как
г) Совершенно аналогично случаю в) получим
Что и требовалось доказать. Определение 15. Ядром типа Джексона порядка n называется функция
n =1,2,3,..., k -натуральное, где
Ядра типа Джексона обладают следующими свойствами:
а)
б) При фиксированном натуральном k и произвольном n ядро J n,k ( t ) является чётным неотрицательным тригонометрическим полиномом порядка k ( n -1)
в)
г) При любом s >0 имеет место неравенство
д) При любом натуральном
Доказательство свойств ядер типа Джексона. а) Это свойство вытекает из равенств определения б) Это свойство следует из 1-го неравенства определения и из того, что в силу равенств (1.11) и (1.11‘’) будет
где
в) Учитывая неравенства (**), будем иметь
С другой стороны
г) Это неравенство вытекает из первого равенства определения и неравенства (1.15‘)
д) Действительно, с одной стороны, в силу неравенств (1.15‘) и (**)
где A-const , а с другой стороны, учитывая соотношение (1.15), неравенств (**) и из неравенства sin t Ј t , при всех t і 0 (***), имеем
A 1 -const . Неравенства (1.16) и (1.16‘) равносильны условию, что и требовалось доказать.
§ 2. Простейшие свойства модулей нерперывности. Этот параграф носит вспомогательный характер. Здесь устанавливается несколько простейших свойств модуля нерперывности высших порядков. Все рассматриваемые здесь функции f 1 , f 2 , ... - непрерывны. ЛЕММА 1. Для любого натурального k и любого d і 0
Доказательство: по определению,
Лемма доказана. ЛЕММА 2. Пусть f и l -натуральные числа, l<k. Тогда для любого d і 0
и
Доказательство: Положим
Тогда для 0 Ј l<k имеем
откуда
Отсюда при l =0 вытекает, что
а при 0< l < k
Полагая в (2.3) l =1, находим, что
Из этого неравенства видно, что для любого натурального k
ЛЕММА 3. Для любого натурального
k
модуль непрерывности
k
-го порядка
Доказательство:
Пусть
Отсюда
и
Таким образом
и так как
ЛЕММА 4. Пусть k и p -натуральные числа. Тогда для любого d і0
Доказательство: Индукция по k даёт формулу
Отсюда
и
Лемма доказана. ЛЕММА 5. Пусть k -натуральное число, d >0, h >0. Тогда
Если кроме того 0< d < h , то
Доказательство: Докажем сперва неравенство (2.6). Рассмотрим случай для hЈd . Найдём натуральное число p из условий
Тогда
h<
p
d
-1
, и так как
Рассмотрим случай для h<d . Найдём натуральное число p из условий
Тогда
h<
p
d
, и так как
и неравенство (2.6) доказано. Неравенство (2.7) вытекает из (2.6), так как d+hЈ2h для 0< d < h . Неравенство (2.7) показывает, что для любой f є 0 и любого натурального k
Лемма доказана. ЛЕММА 6. Пусть f имеет r-ю производную f (r) . Тогда
и для любого натурального k
Доказательство: Оба неравенства непосредственно вытекают из формулы
§3 . Обобщение теоремы Джексона. Здесь будет получено небольшое усиление теоремы Джексона о наилучших приближениях периодических функций тригонометрическими полиномами. Лемма 7. Пусть дано натуральное число k . Существует последовательность ядер {K n ( t )}( n =0,1,...), где K n ( t ) есть тригонометрический полином порядка не выше n , удовлетворяющая условиям:
Эту лемму можно считать известной. Как показывает простой подсчет, совершенно аналогичный проводившемуся Джексоном, в качестве ядер K n ( t ) можно взять ядра Джексона достаточно высокой степени, то есть положить
где
k
0
-целое, не зависит от
n
,
а b p выбираются так, чтобы была выполнена нормировка (3.1). Лемма 8. Если последовательность ядер { K n ( t )} удовлетворяет всем условиям предыдущей леммы, то
Доказательство. Имеем, пользуясь (3.2) и (3.3)
Лемма доказана. Теорема 1. Пусть k -натуральное число. Тогда
Доказательство. Пусть последовательность ядер { K n ( t )} ( n =1,1,2,...) удовлетворяет всем условиям леммы 7. Положим
Очевидно,
Поэтому
Оценим последний интеграл. Полагая в неравенстве (2.6)
Отсюда и из (3.4) следует:
Подставляя эту оценку в (3.6), получаем утверждение теоремы. Теорема доказана. Следствие 1.1. Пусть k -натуральное число, r -целое неотрицательное. Тогда
В самом деле, согласно (2.12)
и применение теоремы 1 даёт (3.7).
§4 . Обобщение неравенства С.Н.Бернштейна. В этом параграфе формулируется одно обобщение неравенства С.Н.Бернштейна для производных от тригонометрического полинома.
Теорема 2.
Пусть
и неравенство обращается в неравенство в том и только в том случае, если
Доказательство этого неравенства опубликовано в работе С.Б.Стечкина [2]. Отметим несколько следствий из этого неравенства. Следствие 2.1. (неравенство С.Н.Бернштейна):
Полагая в (4.1)
(это неравенство доказано С.М.Никольским [5]) но по лемме 2 §2 ,
откуда и следует (4.2). Два последних неравенства одновременно обращаются в равенство только в случае, если
Следствие 2.2. Пусть
Первое неравенство совпадает с утверждением теоремы 2, а второе вытекает из оценки
Таким образом, для
Следствие 2.3.
Пусть
В частности,
Следствие 2.4.
Пусть
В частности, для
В самом деле, из (4.4) или (2.12) следует:
и остается воспользоваться неравенством (4.5).
Следствие 2.5.
Пусть
Вторая половина неравенства совпадает со следствием 2.4, а первая непосредственно вытекает из (2.7).
§5 . Дифференциальные свойства тригонометрических полиномов, аппроксимирующих заданную функцию. В этом параграфе устанавливается, что если тригонометрический полином t n ( x ) близок к заданной функции f , то его модули непрерывности можно оценить через модули непрерывности f . Теорема 3. Зафиксируем натуральные числа k и n и пусть
Тогда для любого
и
Предварительные замечания.
Неравенства (5.2) и (5.4) предпочтительнее для больших
d
, а (5.3)-для малых. Если
Доказательство. Докажем (5.2). Пользуясь (2.1), (2.2) и (5.1), имеем
Докажем (5.5). Положим в (5.2)
после чего (4.5) даёт (5.5). (5.3) следует из (5.5) в силу (2.11).
Остаётся доказать (5.4). Пусть сперва
Рассмотрим, наконец, случай
Подставляя эту оценку в (5.3), получаем (5.4) для
Таким образом, теорема полностью доказана. Следствие 3.1. Пусть для некоторого натурального k и любого натурального n
Тогда для любого d >0
равномерно относительно n . Следствие 3.2. Пусть для некоторого натурального k и любого натурального n
Тогда
Теорема 4.
Для того, чтобы
равномерно относительно n.
Это вытекает из теоремы 1, следствия 3.1 и того замечания что если выполнено условие (5.9), то
Теорема 5.
Для того, чтобы
Это доказывается аналогично теореме 4, только вместо следствия 3.1 нужно воспользоваться следствием 3.2. Неравенства теоремы 3 имеют тот недостаток, что их правые части явно зависят от константы С 20 . Таким образом, если вместо фиксированного номера n и одного полинома t n рассматривать последовательность полиномов { t n } ( n =1,2,...), то С 20 окажется, вообще говоря, независящей от n и теорема 3 даёт оценки, не равномерные относительно n . Покажем как избавиться от этого неудобства. Теорема 6. Пусть для некоторого натурального k
и
Тогда для любого d >0
равномерно относительно n .
Доказательство.
Пусть сперва
и на основании (5.11)
Рассмотрим случай
Из этого неравенства, в силу (4.7), следует, что
Но так как, по условию,
Отсюда
Окончательно,
и теорема доказана. В следующем параграфе будет показано, как можно видоизменить ограничения (5.11) теоремы 6.
§6. Обобщение обратных теорем С. Н. Бернштейна и Ш. Валле-Пуссена. В этом параграфе обобщаются и уточняются так называемые “обратные теоремы” теории приближения. Речь идёт об оценке дифференциальных свойств функции f , если известны свойства последовательности её наилучших приближений { E n }. Лемма 9. Зададим натуральное число k , и пусть
и
Тогда
Доказательство. Имеем, согласно (2.1),
Но из (2.10) и (6.2) получаем
а из (2.2) и (6.1)
Поэтому
левая часть этого неравенства не зависит от n , а поэтому
и лемма доказана.
Для получения хороших оценок
Теорема 7.
Пусть
k
-натуральное число, функция
Для того чтобы
Доказательство. Необходимость условия (6.5) вытекает из следствия 3.2. Установим его достаточность, для чего воспользуемся леммой 9. Получаем:
Положим здесь
и теорема доказана. Отметим два следствия из этой теоремы.
Следствие 7.1.
Пусть
k
-натуральное число, функция
Для того чтобы
Следствие 7.2.
Пусть
k
-натуральное число и
и
то
равномерно относительно n . Это вытекает из теорем 7 и 6.
Теорема 7 показывает, что нужно добавить к условию (6.4), чтобы получить
Лемма 10. Пусть
где
Доказательство. Зафиксируем натуральное число n , определим натуральное p из условий
и построим последовательность номеров
Для оценки
Так как
Оценим U l (k) . Имеем для l= 1,2,..., p
откуда
Но
Заметим теперь, что, в силу определения последовательности { n l },
Поэтому, пользуясь ещё монотонностью последовательности {
F
n
}
2
находим, что для
При помощи (6.11), (6.12) и (6.13) находим окончательно:
и лемма доказана.
Теорема 8.
Для любого натурального
k
и любого
Доказательство. Имеем
Отсюда, по лемме 10,
Воспользуемся теперь леммой 9. Получаем:
Если
Поэтому для
и теорема доказана.
Мы обращаемся теперь к рассмотрению вопроса о том, при каких ограничениях на {
E
n
} условие (6.4) влечёт
Теорема 9.
Зададим натуральное число
k
; пусть
Доказательство.
Необходимость условия (6.15) вытекает из теоремы 1. Докажем его достаточность. Согласно теореме 8, для
Положим здесь
Поэтому для
и теорема доказана.
Следствие 9.1.
Пусть
Следствие 9.2.
Пусть
то для любого фиксированного натурального
равномерно относительно n . Рассмотрим теперь следующий вопрос. как связаны приближения функции f с приближениями и дифференциальными свойствами её производных f (r) ? Теорема 10. Зададим натуральное число r, и пусть
где
Тогда f имеет непрерывную производную f (r) и
С.Н.Бернштейн [3] доказал такую теорему: если ряд
Доказательство.
Зафиксируем натуральное число n и положим
Тогда будем иметь
где
Докажем, что формулу (6.19) можно продифференцировать почленно r раз, т.е.
Для этого достаточно установить, что ряд справа равномерно сходится. Прежде всего, оценим
откуда
Оценим теперь
Пользуясь этой оценкой, получаем:
Но
Поэтому
Итак, доказана сходимость ряда
и теорема доказана. В некоторых случаях оценка (6.18) может быть упрощена. Пусть, например,
Тогда
Поэтому при выполнении условия (6.22) вместо (6.18) можно написать
Следствие 10.1. Пусть r -натуральное число и сходится ряд
Тогда
Теорема 11. Пусть r -натуральное число и для функции f сходится ряд
Тогда для любого натурального
k
и любого
Доказательство. Имеем
Отсюда, по лемме 10,
Далее, согласно теореме 10,
Воспользуемся теперь леммой 9. Получаем
Заметим, что
Таким образом, если
и теорема доказана. §7. Основная теорема. Обратимся теперь к рассмотрению следующего вопроса: каковы необходимые и достаточные условия того, чтобы
где
Насколько нам известно, эта задача не была до сих пор решена даже для случая
Лемма 11.
Пусть
Тогда существует такая константа с >0, что
Доказательство. Согласно (7.1), найдутся две такие константы С 60 >0 и C 61 >0, что
Последнее из этих неравенств, теорема 1 и теорема 3 влекут неравенство
В силу (2.1) и (2.2), имеем
Отсюда
Пользуясь (7.3) и (7.4), находим, далее
Вспомним теперь, что
Подставляя эту оценку в (7.5), получаем
Мы можем без ограничения общности считать, что здесь
Тогда получим окончательно
и лемма доказана.
Основная теорема.
Пусть
необходимо, чтобы для всех натуральных
Доказательство. Пусть имеет место (7.7), т.е. найдутся две положительные константы С 67 и С 68 , для которых
Тогда, по теореме 1 и в силу первой половины неравенства (7.9), для любого k имеем
т.е.
Отсюда, в силу
и если
Далее, из второй половины неравенства (7.9) и теоремы 9 вытекает существование константы
С
72
такой, что для любого
Этим заканчивается доказательство необходимости условия (7.8). Пусть имеет место (7.8):
с С 73 >0. Тогда по теореме 1 и в силу второй половины неравенства (6.10),
а по лемме 11,
где С 77 >0. Таким образом, установлена достаточность условия (7.8), и основная теорема полностью доказана.
Приведём в заключение обобщение леммы 11 на тот случай, когда оценки
Теорема 12.
Пусть
Тогда
Доказательство. Имеем, как при доказательстве леммы 11,
Положим здесь
Тогда получим, что
Теорема доказана.
§8. Решение задач. Пример 1. Пусть
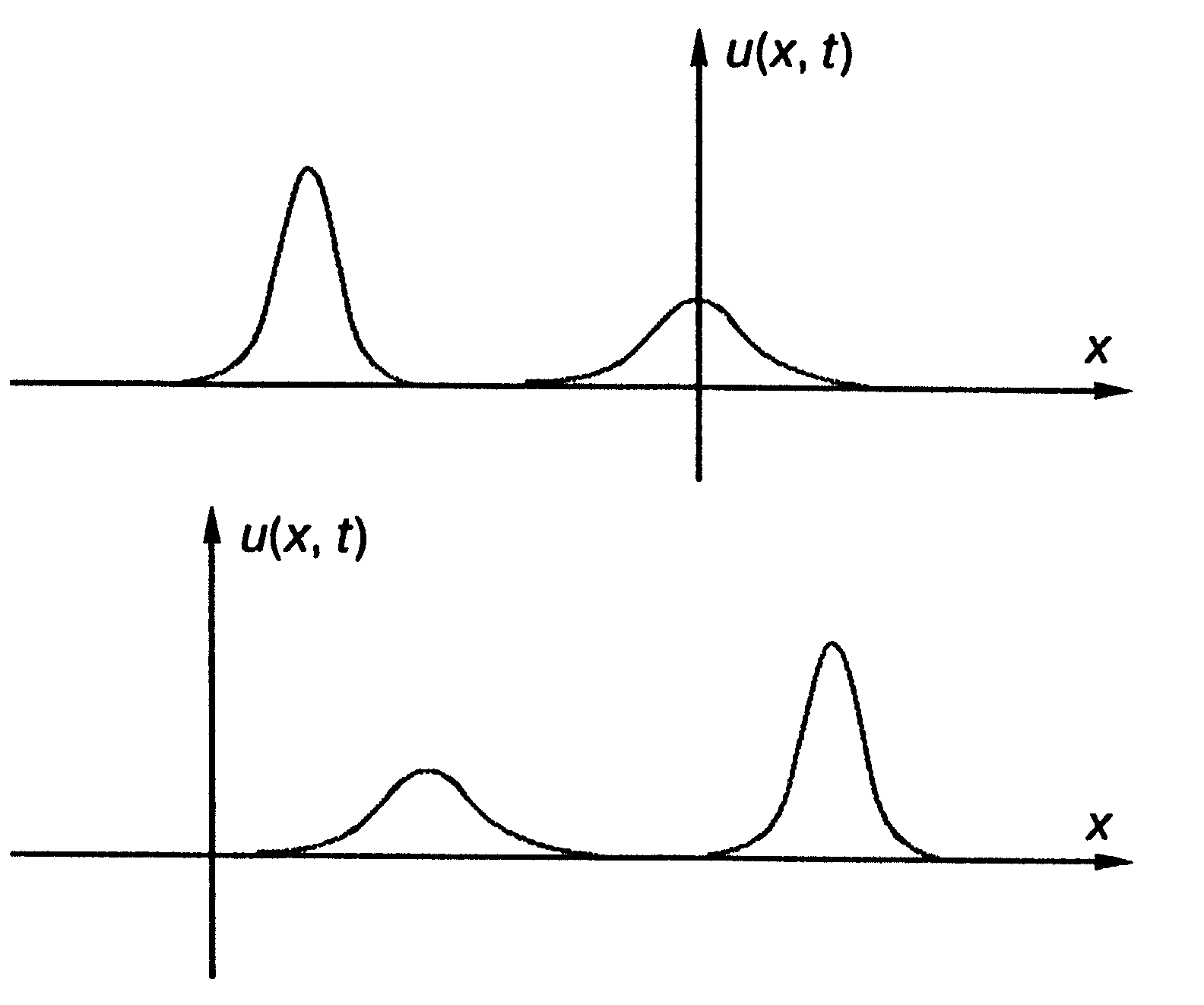
Пример 2. Пусть график функции f ( x ) имеет вид, изображённый на рис.8.1. Тогда график функции
Рис. 8.1. Рис. 8.2.
Пример 3.
Пусть при
и пусть
Рис. 8.3.
Тогда если функцию
то (рис. 8.4)
т.е. модуль непрерывности функции
Пример 4.
При
является модулем непрерывности.
Пример 5
. При
является модулем непрерывности.
Пример 6.
При
Литература.
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
 .
.
 ,
,
 ;
;
 .
.
 .
.

 (1.1)
(1.1)
 (1.1’)
(1.1’)

 (1.4)
(1.4)
 (1.4’)
(1.4’)


 (1.6)
(1.6)
 .
.


 (1.7)
(1.7)





 Этим неравенство (1.8) доказано. Неравенство (1.8’) следует из монотонности функции
w
k
(
t
) и неравенства (1.8).
Этим неравенство (1.8) доказано. Неравенство (1.8’) следует из монотонности функции
w
k
(
t
) и неравенства (1.8).


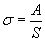 (1.10)
(1.10)
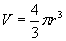 (1.11)
(1.11)
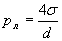 (1.12)
(1.12)
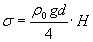 ,
,
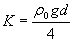
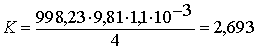
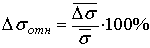
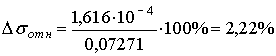 получим
получим
 , (1.13)
, (1.13)
 (1.13’)
(1.13’)
 (1.14)
(1.14)
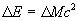 (1.15)
(1.15)
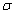 (1.15‘)
(1.15‘)
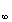
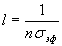 (1.16)
(1.16)
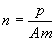 (1.16‘)
(1.16‘)
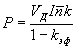

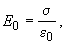
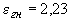
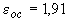 Если
k
=0, то мы получаем формулу (2.11). Лемма доказана.
Если
k
=0, то мы получаем формулу (2.11). Лемма доказана.
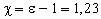 (3.1)
(3.1)
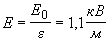 (3.2)
(3.2)
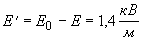 (3.3)
(3.3)
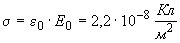
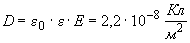 (3.4)
(3.4)
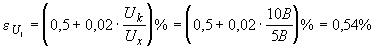
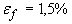
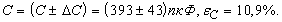
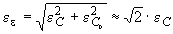 (3.6)
(3.6)
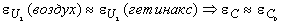 , получим, что
, получим, что
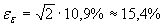

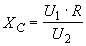 (4.1)
(4.1)
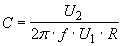
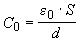
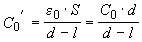 (4.3)
(4.3)
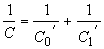 средний член в (4.3) заключен между двумя пределами, зависящими только от
q
.
средний член в (4.3) заключен между двумя пределами, зависящими только от
q
.
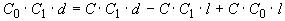 (4.5)
(4.5)
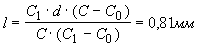 (4.6)
(4.6)
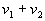 (4.7)
(4.7)
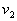 (4.8)
(4.8)
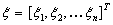 . (4.9)
. (4.9)
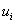 (5.3)
(5.3)
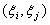 (5.4)
(5.4)
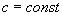 (5.5)
(5.5)
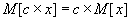
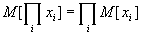
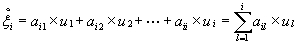 (6.10)
(6.10)
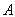

 (6.11)
(6.11)
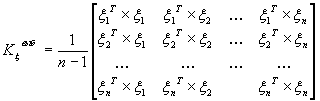 (6.13)
(6.13)
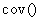
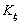 (6.14)
(6.14)
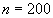
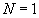
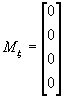
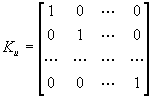
 (6.17)
(6.17)
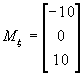 (6.18)
(6.18)
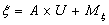
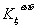 (6.19)
(6.19)
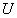 (6.20)
(6.20)
 (6.21)
(6.21)
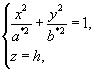
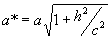
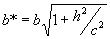
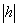 (6.23)
(6.23)
 (6.24)
(6.24)

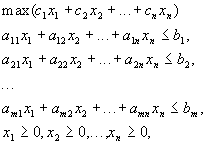
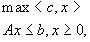
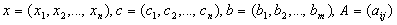
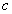
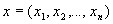 (7.4)
(7.4)
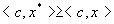 (7.5)
(7.5)
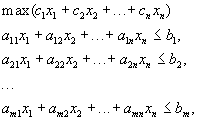 (7.6)
(7.6)
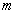

 (7.12)
(7.12)

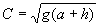
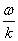
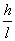
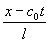
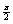 - периодическое продолжение функции
- периодическое продолжение функции
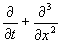
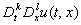 Рис. 8.4.
Рис. 8.4.
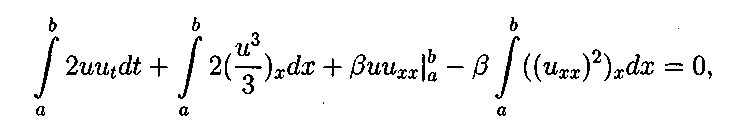
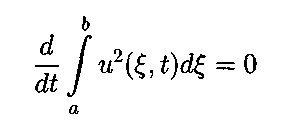
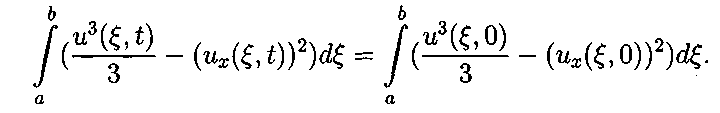
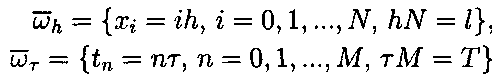
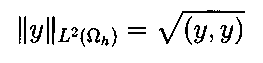 .
.
 Главная
Главная