Варианты проверочных работ
Вариант 1 Решите уравнения (1—3): Задание 1.
Задание 2. (х2 + х + 1)(х2 + х + 2) = 12. Задание 3.
Задание 4. На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют неравенствам
Задание 5. Найдите а, если сумма квадратов корней уравнения х2 + 4х; + а = 0 равна 18. Задание 6. Пусть х1 и х2 корни уравнения х2 + рх + q = 0 Составьте квадратное уравнение, корнями которого являются
Задание 7. При каких о оба корня уравнения (3 - х)(х + 1) = а положительны? Задание 8. Найдите все а, при которых неравенство х2 + (а - 1)х + а - 2а2< 0 имеет только положительные решения.
Вариант 2 Решите уравнения (1—3): Задание 1.
Задание 2. (х2 + З)2 - 7(х4 - 9) + б(х2 - З)2 = 0. Задание 3.
Задание 4. На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют неравенствам
Задание 5. Составьте квадратное уравнение, произведение корней которого х1 и х2 равно 4, а
Задание 6. Найдите все а, при которых оба корня уравнения х2 - 2ах + а2 - 1= 0 принадлежат интервалу (-2; 4). Задание 7. При каких а функция
убывает на отрезке [8а; а + 8]? Задание 8. При каких значениях а неравенство ах2 + 4х + За -- 1> 0 выполняется для всех
Вариант 3 Задание 1.
Задание 2.
Задание 3.
Задание 4. Найдите все а, при которых корни уравнения х2 + (а + 2)х + За + 1 = 0 действительны и сумма их кубов меньше, чем 5а - 2. Задание 5. Найдите все значения параметра а, при которых система
имеет хотя бы одно решение. Задание 6. Найдите все значения а, при которых неравенство
выполняется для всех х € [-1; 1]. Задание 7. При каких а корни уравнений х2 + Зх + 2а = 0 и х2 + 6х + 5а = 0 различны и перемежаются? Задание 8. При каких а наименьшее значение функции у = х2 + (а - 2)х - а на отрезке [1; 3] равно (-4)? Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
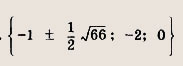
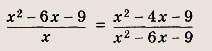
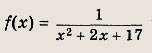
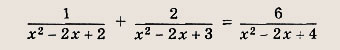
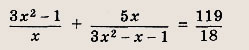
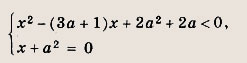
Главная| Разрешается частичное копирование контента в виде анонса при условии размещения прямой ссылки на источник. | © 2006-2024 «Claw.RU» © 2006-2024 «Рефератики.РФ» |