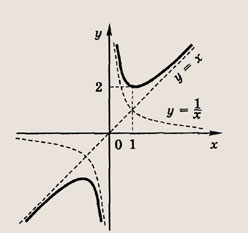
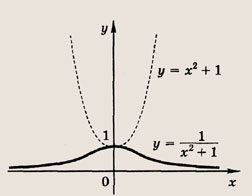
Прямая, окружность,
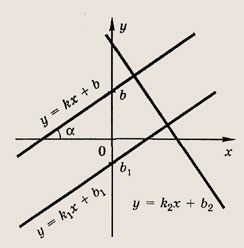
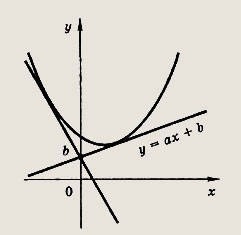
парабола и гипербола. • Уравнение вида ах + bх + с = 0 называется общим уравнением прямой. Мы уже знаем, что каждая прямая записывается таким уравнением и, обратно, каждое такое уравнение определяет прямую. Если уравнение прямой записано в виде у = kx + b, то число k называется ее угловым коэффициентом. При этом
т.е. совпадает с тангенсом угла наклона прямой L к оси Ох
Признаком параллельности двух прямых L и L1 является равенство их угловых коэффициентов: k = k1. Признаком перпендикулярности прямых L и L2 является соотношение kk2 = -1. Наконец, уравнение y - y0 = k(x
- x0)
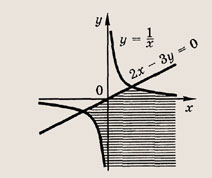
— уравнением прямой, проходящей через две данные точки А(х0; у0) и В(х1; y1). Задание 1. Определите точки пересечения прямой 2х - Зу -- 6 = 0 с координатными осями и постройте эту прямую. Ответ: А(3; 0), В(0; -2) Задание 2. Запишите уравнение прямой, проходящей через данную точку А(х0; у0) и образующей с осью Ох угол
а) в)
Ответ: а) б) в) Задание 3. Запишите уравнение прямой, параллельной прямой у = 2х + 3 и проходящей через точку А(-3; 2). Ответ: у = 2х + 8 Задание 4. Запишите уравнение прямой, перпендикуляр,ной прямой у = -5х + 3 и проходящей через точку А(5;4) Ответ:
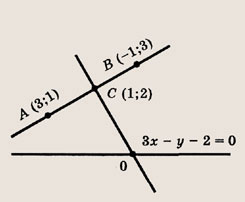
Задание 5. Запишите уравнение сторон треугольника, если известны его вершины А(5; -4), В(-1; 3) и С(-3; -2). Решение: Используя общее уравнение прямой, проходящей через две заданные точки, для прямой (АВ) имеем
т. е. 7х + 6у - 11 = 0. Аналогично получаем: (АС) х - 4у + 11 = 0, (ВС) 5х - 2у + 11 = 0.
Запишите уравнение прямой, проходящей через точку М1(2, 1) перпендикулярно прямой, проходящей через точки М2(5; 3) и М3(3; -4). • Пусть А(х0; у0), B(х1у1) — две данные точки; тогда точка С
лежит на прямой, проходящей через точки А и В, и делит отрезок АВ пополам. Используйте этот факт при решении задний 7, 8. Решение: Уравнение прямой (М2М3) имеет вид 7х - 2у - 29 = 0. Ее угловой коэффициент равен
Поэтому уравнения прямых, перпендикулярных данной прямой, имеют вид
Подставляя в это равенство координаты точки М1 (2; 1), находим
Отсюда следует нужное нам уравнение. Ответ: 2х + 7у - 11=0 Задание 7. Найдите координаты точки О, симметричной тс)чке Р(-5; 13) относительно прямой 2х - Зу - 3 = 0. Решение: Проведем через точку Р (-5; 13) прямую, перпендикулярную прямой 2х -Зу - 5 = 0. Ее уравнение есть Зх + 2у - 11 = 0. Найдем координаты точки пересечения этих прямых, для чего решим систему уравнений
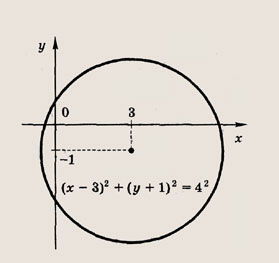
откуда Q(11l; -11). Ответ: Q (11;-11) Задание 8. Составьте уравнение прямой, параллельной прямым 2х + Зу -6 = 0 и 4х + 6у+ 17 = 0 и проходящей посередине между ними. • Уравнение (х - х0)2 + (у - у0)2 = R2 определяет окружность радиуса R с центром в точке С(х0; у0). Решение: Прямая 2х + Зу - 6 = 0 проходит через точку А(0; 2), а прямая 4х + 6у + 17 = 0 — через точку В
Следовательно, прямая, параллельная данным и проходящая посередине между ними, имеет уравнение 2х + Зу + 6 = 0 и проходит через точку C
где С — середина отрезка АВ. Отсюда находим
а тогда уравнение искомой прямой можно записать в виде: 8х + 12у + 5 = 0. Заметим, что это уравнение есть полусумма уравнений 8х + 12у - 24 = 0 и 8х + 12у + 34 = 0, задающих известные нам прямые. Ответ: 8х + 12у + 5 = 0 Задание 9. Запишите уравнение окружности, если: а) центр окружности совпадает с точкой С(2; -3), а ее радиус R = 7; б) окружность проходит через точку А(2; 6), а ее центр совпадает с точкой С(-1; 2); в) точки А(3; 2) и В(-1; 6) являются концами одного из диаметров этой окружности. Ответ: а) (х - 2)2 + (у + З)2 = 49; б) (х + 1)2 + (у - 2)2 = 25; в) (х - 1)2 + (у - 4)2 = 8 Задание 10. Запишите уравнение окружности, если ее центр совпадает с началом координат, а прямая Зх - 4у + 25 = 0 является касательной к этой окружности. Решение: Через начало координат О (0; 0), т. е. через центр окружности, проведем прямую, перпендикулярную прямой Зх - 4у + 25 = 0. Ее уравнение имеет вид 4х + Зу = 0. Найдем точку пересечения этих прямых, т. е. точку касания прямой Зх - 4у + 25 = 0 и искомой окружности. Решаем систему
откуда х = 3, у = -4. Таким образом, С(3; -4) — точка касания, а
— радиус искомой окружности. Ответ: х2 + у2
= 25 Запишите уравнение окружности, проходящей через точки А(3; 1) и Б(-1; 3), если ее центр лежит на прямой Зх - у -2 = 0. Решение: Центр искомой окружности О (х0; у0) - точка пересечения прямой Зх - у - 2 = 0 и прямой, проходящей через точку С(1;2) (середину отрезка АВ), перпендикулярно прямой (АВ)
Ее уравнение имеет вид у - 2х = 0 (см. решение задачи 6). Тогда
откуда О (2; 4). Радиус искомой окружности равен длине отрезка ОВ, т. е.
Ответ: (х - 2)2 + (у - 4)2 = 10 Задание 12. Запишите уравнение прямой, проходящей через центры двух данных окружностей: а) (х - З)2 + у2 = 9, (х + 2)2 + (у -1)2 = 1; б) х2 + у2 - 4х + 6у = 0, х2 + у2 - 6х = 0. Ответ: а) х + 5у - 3 = 0; б) 3х - у - 9 = 0 Задание 13. Запишите уравнения касательных к окружности х2 + у2 + + 2х - 19 = 0, проведенных из точки А (1; 6). Указание: Запишите уравнения искомых прямых в виде у = а(х - 1) + 6, подставьте у = а(х — 1) + 6 в уравнение окружности и приравняйте нулю дискриминант полученного квадратного уравнения. Ответ: у + 2х - 8 = 0, х - 2у + 11 =0. Задание 14. Установите, что каждое из следующих уравнений определяет параболу, найдите координаты ее вершины А и координаты точек пересечения с осями координат: а) б) в) Ответ: а) А(1; 3); с осью Ох не пересекается; С (0; 7); б) А(-2; -3);
в) А(1; 4); В1(-1; 0); В1(3; 0); С(0; 3). Задание 15. Найдите квадратный трехчлен, наибольшее значение которого, равное 3, достигается при х = 2, если известно, что его график проходит через точку О(0; 0). Решение: Из условия следует, что квадратный трехчлен имеет вид у = а(х - 2)2 + 3, где а < 0. Подставляя в это равенство х = 0 и у = 0, получаем
Ответ:
Задание 16. График квадратного трехчлена, свободный член которого равен 1, симметричен относительно прямой х + 2 = 0 и проходит через точку А(2; 7). Запишите этот квадратный трехчлен. Ответ:
Задание 17. Найдите квадратный трехчлен, график которого симметричен относительно прямой х = -1 и проходит через точки М1(-2; 2) и М2(2; 26). Решение: Из условия следует, что квадратный трехчлен имеет вид у = а(х + 1)2 + b. Подставляя в это равенство координаты точек М1(-2; 2) и М2(2; 26), получаем систему
Ответ: у = = 3х2+ 6х + 2 Задание 18. Найдите квадратный трехчлен, график которого симметричен относительно прямой х = 1 и проходит через точки M1(2; -1) и М2(-4; 47). Ответ: у = 2х2 - 4х - 1 Задание 19. Парабола у = х2 - 4х + 2 пересекается с прямой у = х + 8 в точках А и В. Запишите уравнение параболы, проходящей через А, В и точку О(0; 0). Решение: Находим координаты точек А и В. Решаем уравнение х2 - 4х + 2 = х + 8, т. е. х2 - 5х - 6 = 0 и получаем: А (-1; 7), В (6; 14). Уравнение искомой параболы имеет вид у = ах2 + bх. Подставляя в это равенство координаты точек А и В, приходим к системе:
Ответ:
Задание 20. График квадратного трехчлена, наименьшее значение которого, равное нулю, достигается при х - 1, проходит через точку А(-1; 4). Составьте уравнения касательных к этому графику, проходящих через начало координат. Решение: Из условия следует, что квадратный трехчлен имеет вид у = а(х - 1)2, где а > 0. Подставляя в это равенство координаты точки А (-1; 4), находим а = 1, откуда у = (х - 1)2 = х2 - 2х + 1. Уравнения всех прямых, проходящих через точку О (0; 0), имеют вид у = ах. Приравнивая нулю дискриминант квадратного уравнения х2 - 2х + 1 = = ах, т. е. х2 - (2 + а)х + 1 = 0, имеем D = (а + 2)2 - 4 = а2 + 4а = О, откуда a1= 0, а2 = -4. Таким образом, получаем искомые уравнения касательных: у = 0 и у = -4х. Ответ: у = 0, у = -4х Запишите уравнение параболы, проходящей через данные точки А, В и С, если: а)А(0;-1),В(1; 1), С(-1; 2); б)А(-1;0}, В(1;4), С(2; 3). • Функция вида
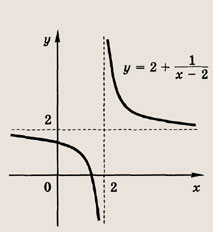
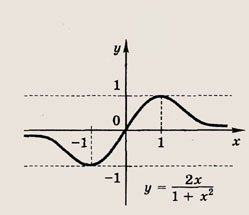
где
a, b, d — действительные числа и
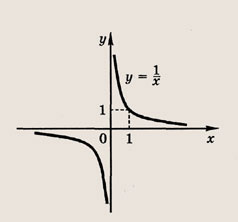
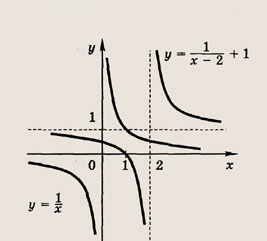
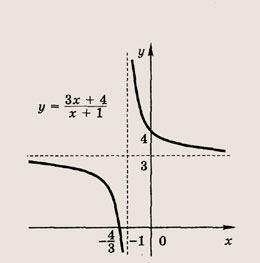
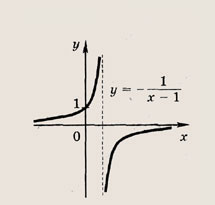
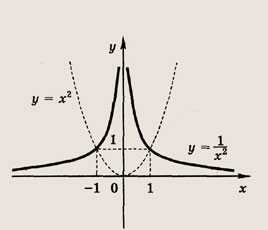
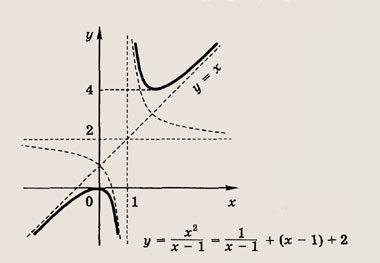
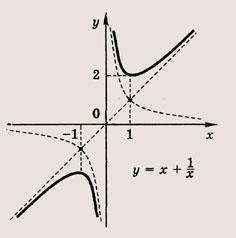
называется дробно-линейной функцией. Кривая, которая служит графиком этой функции, называется гиперболой. Ниже мы установим, что график дробно-линейной функции можно получить из графика простейшей дробно-линейной функции
(графика обратной пропорциональной
зависимости) с помощью параллельного переноса,
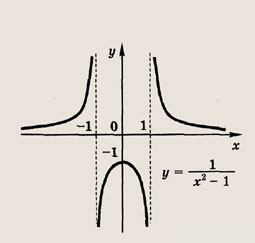
Отметим, что прямые у =0 и х=0 (координатные оси) являются асимптотами гиперболы
а точка О(0; 0) — ее центром симметрии. Указание: Запишите уравнение искомой параболы в виде у = ах2 + bх + с и подставьте в это равенство координаты данных в условии точек. Ответ: а) у = 2х2- х - 1; б) у = -х2 + 2х + 3 Постройте графики следующих функций и уравнений. Штриховкой укажите области, координаты точек которых удовлетворяют указанным неравенствам (22—26):
Задание 22.
Ответ:
Задание 23.
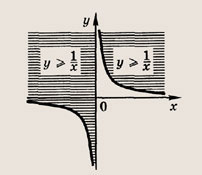
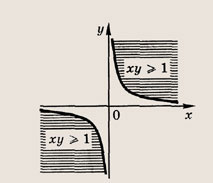
Почему в заданиях 22 и 23 получаются различные заштрихованные области? Ответ:
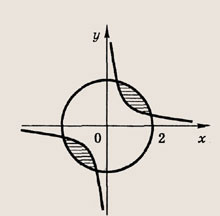
Задание 24.
Ответ:
Задание 25.
Ответ:
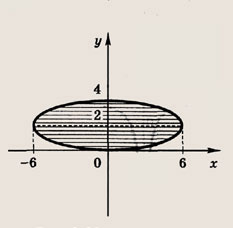
(эта кривая также является гиперболой). Ответ:
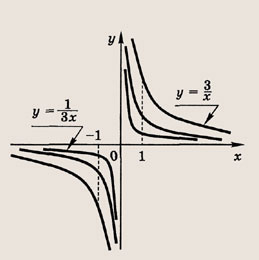
Задание 27. Составьте уравнения касательных к гиперболе
параллельных прямой у = -4х + 1.
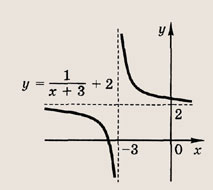
• Сдвиги (параллельные переносы) вдоль координатных осей. Пусть построен график функции у = f(x). Тогда: 1) график функции у = f(x
+ а) получается из графика функции у - f(x) переносом вдоль оси Ох на а единиц 2) график функции у = f(x) + b получается из графика функции у = f(x) переносом на b единиц вверх, если b > О, или на |b| = -b единиц вниз, если b < 0; 3) график уравнения f(x -а, у) = О получается из графика уравнения f(x, у) = О переносом на |а| вправо, если а > 0, и влево, если а < 0. Аналогичное правило справедливо и для аргумента у, т. е. график f(x, у - b) = О получается из графика f(x, у) = 0 переносом на |b| единиц вверх, если b > 0, и вниз, если b < 0. Решение: Уравнение касательной должно иметь вид у = -4х+ b. Приравнивая нулю дискриминант квадратного уравнения
Ответ: у = -4х - 4; у = -4x + 4 Постройте графики следующих функций и уравнений (28—34):
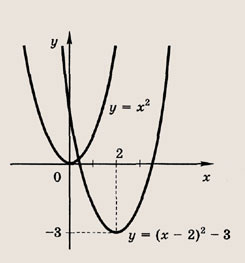
у = х2; у = (х - 2)2; у = (х -2)2 - 3 Ответ:
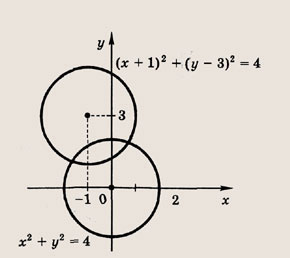
Задание 29. х2 + у2 = 4; (х + 1)2 + у2 = 4; (х + 1)2 + (у - З)2 = 4 Ответ:
Задание 30..
Ответ:
Задание 31.
Ответ:
Задание 32. х2 - 6х + у2 + 2у - 6 = 0 Ответ: Задание 33. (jc - 1)(у + 2) = 2х - 3 Указание: Преобразуйте уравнение к виду
Ответ:
Задание 34. ху + Зу - 2х = 7 Указание: Преобразуйте уравнение к виду
Ответ:
Задание 35. Даны окружности: а) (х - 1)2 + (у + 1)2 = 4; б) х2 - 4х + у2 + 6у = 0 Запишите уравнение образа каждой из них при параллельном переносе, если ее центр смещается в точку С(-1; 2). Решение б): Запишем уравнение данной окружности в виде (х - 2)2 + (у + З)2 = 13. При параллельном переносе радиус окружности не меняется. Уравнение окружности радиуса
с центром в точке С(-1;2) имеет вид (х + 1)2 + (у - 2)2 = 13. Ответ: а) (х + 1)2 + (у - 2)2 = 4 б) (х + 1)2 +
(у - 2)2 = 13 Запишите уравнение образа параболы у = х2 + + 2х + 2 при параллельном переносе, если ее вершина смещается в точку A(x0; у0), где а) А(0; 0); б) А(-3; 4); в)А(-1; 1). Решение б). Парабола у = х2 + 2х + 2 = (х + 1)2 + 1 получается из параболы у = х2 переносом вершины в точку А (-1; 1). Если вершина этой параболы при параллельном переносе сместится в точку А (-3; 4), то ее уравнение примет вид у = (х + З)2 + 4. а) у = х2 б) у = х2 + 6х + 13 в) у = х2 + 2х + 2 Ответ:
Запишите уравнение образа гиперболы
при параллельном переносе, если ее центр симметрии смещается вточку А(-3; 1). • Зеркальное отражение относительно координатных осей. Пусть задан график функции у = f(x) (или уравнения f(x, у) = 0). Тогда: 1) графики функций у = f(x) и у = f(-x) (уравнений f(x, у) = 0 и f(-x, у) = 0) симметричны относительно оси Оу, 2) графики функций у = f(x) и у = -f(x) (уравнений f(x, у) = 0 и f(x; -у) = 0) симметричны относительно оси Ох. Постройте графики следующих функций и уравнений (38—42). Ответ:
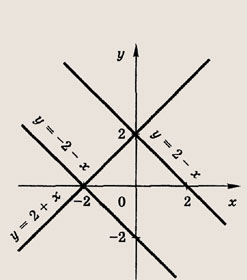
Задание 38. у = 2 + х; у = 2 - х; у = -(2 + х) Ответ:
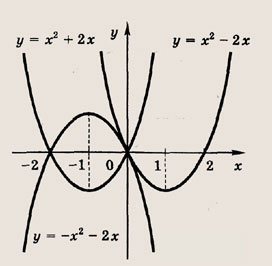
Задание 39. у = х2 + 2х; у = х2 - 2х; у = -(х2 + 2х) Ответ:
Задание 40.
Ответ:
Задание 41. Ответ:
Задание 42. (х - I)2 + у2=1;(х + 1)2 + у2=1
Пусть задан график функции у = f(x) и число k > 0. Тогда: 1) график функции у = f(kx) получается из графика функции у = f(x) сжатием вдоль оси Ох в k раз, если
(при k < 1 получает растяжение в 1/k раз); 2) график функции у = kf(x) получается из графика функции у = f(x) растяжением вдоль оси Оу в k раз, если
(при k < 1 получаем сжатие в 1/k раз). Отметим также, что графики уравнений f(kx, у) = 0, f(x, ky) = 0 получаются из графика уравнения f(x, у) = 0 сжатием вдоль соответствующей координатной оси в k раз, если k > 1 (при k < 1 получаем растяжение в 1/k раз). Постройте графики следующих функций и уравнений (43—50). Отметьте штриховкой области, координаты точек которых удовлетворяют указанным неравенствам. Ответ:
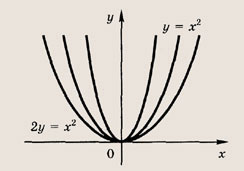
Задание 43. у = х2; у = (2х)2; 2у = х2 Ответ:
Задание 44.
Ответ:
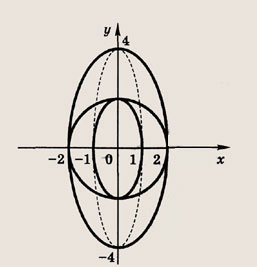
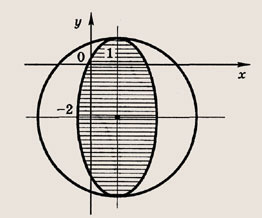
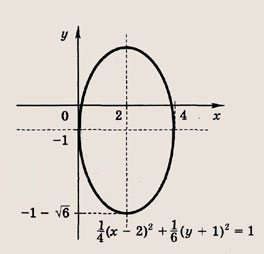
Задание 45.
(кривая, которая получается при сжатии окружности вдоль координатных осей, называется эллипсом). Ответ:
Задание 46.
Ответ:
Задание 47.
Ответ:
Задание 48.
Ответ:
Задание 49.
Ответ:
Задание 50.
• При построении эскизов графиков элементарных функций часто используются и такие приемы, как сложение (вычитание) и деление (умножение) графиков. Постройте графики следующих функций (51—57): Ответ:
Задание 51.
Ответ:
Задание 52.
Ответ:
Задание 53.
Ответ:
Задание 54.
Ответ:
Задание 55.
Ответ:
Задание 56.
Указание:
Ответ:
Задание 57.
Указание:
Ответ:
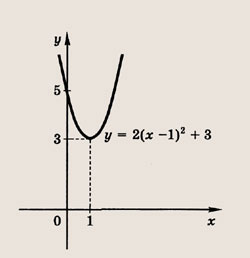
Используя различные приемы, постройте графики следующих функций и уравнений (58—71): Задание 58. у = 2(х- 1)2 + 3 Ответ:
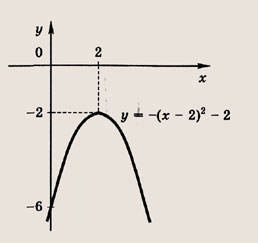
Задание 59. у = 4х - х2 - 6 Указание: у = -(х - 2)2 - 2 Ответ:
Задание 60.
Указание:
Ответ:
Задание 61.
Ответ:
Задание 62.
Ответ:
Задание 63.
Ответ:
Задание 64.
Указание:
Ответ:
Задание 65.
Указание:
Ответ:
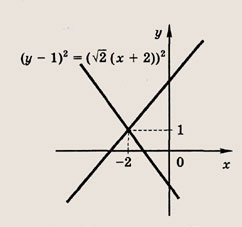
Задание 66. 3(х - 1)2 - 4(у + 1)2 = 0 Указание: Постройте две пересекающиеся прямые Зх2 = 4у2, затем выполните параллельный перенос, при котором точка их пересечения сместится в точку А(1; -1). Ответ:
Задание 67. 2х2 - у2 + 8х + 2у + 7 = 0 Указание:
Ответ:
Задание 68. (х + 2)2 + 4(у - З)2 = 16 Ответ:
Задание 69. Зх2 + 2у2 - 12х + 4у + 2= 0 Указание:
Ответ:
Задание 70. х2 - ху + 1 = 0 Указание:
Ответ:
Задание 71. ху + х - 2у - 4 = 0 Указание:
Ответ:
Найдите число различных решений уравнений в зависимости от а (72—80):
Ответ: При
два решения. Задание 73.
Ответ: При
два решения, при
одно решение; при
нет решений. Задание 74.
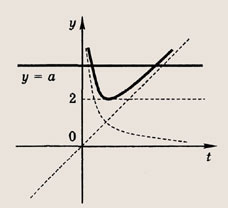
Решение: Положим х2 = t. Тогда
Построим при t > 0 график функции
Так как
при t > 0, причем наименьшее
значение у = 2 достигается при t = 1, то получаем: при
не имеет положительных решений, при а = 2 => одно решение; а > 2 => два решения. Теперь находим число решений исходного уравнения. Ответ: при
нет решений, при а = 2 => два решения; при
четыре решения. Задание 75.
Решение: Построим график функции
Так как
то х = -1 - точки минимума функции у(х) и у(-1) = 3
Поэтому получаем следующий ответ. Ответ: при
одно решение; при а = 3 => два решения; при
три решения. Задание 76. х3 + 2 = ах Указание: Запишите уравнение в виде Ответ: При
одно решение; при а = 3 => два решения; при
три решения. Задание 77. х3 - ах2 + 1 = 0 Указание: Запишите уравнение в виде
Ответ: при
одно решение; при
два решения; при
три решения. Задание 78.
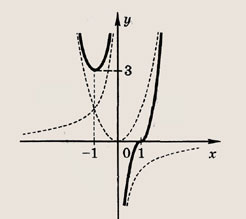
Решение: Имеем
График этой функции — гипербола, принимающая все значения, кроме у = 3, по одному разу. Поскольку
нужно также исключить значение
Ответ: при
одно решение; при
нет решений. Задание 79.
Решение: Запишем уравнение в виде
положим
Заметим, что
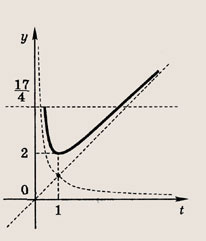
Построим график функции
а наименьшее значение y(t) равно 2. Поэтому уравнение
не имеет решении, при
— имеет одно решение, а при
— два решения, удовлетворяющих условию
Отдельно рассмотрим случай
Уравнение
т. е.
имеет одно решение (мы находим число различных решений). При всех остальных
уравнение х2 + х + 1 = 3t будет иметь два различных решения. Теперь легко записываем ответ. Ответ: при
нет решений; при
два решения; при
четыре решения; при
три решения. (х2 + 1)(х2 + 2ах + а2 + 1) = 2х Указание: Запищите уравнение в виде
и постройте графики функций
Ответ: При
одно решение х = 1, при
других а решений нет. Решите системы неравенств и уравнений (81—87): Задание 81.
Ответ: При
при
при
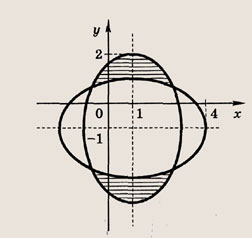
Задание 82.
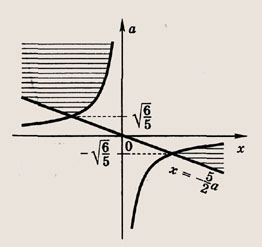
Решение: На координатной плоскости (х, а) штриховкой отметим точки, координаты которых удовлетворяют нашей системе неравенств
Ответ: при
при
при
при
Задание 83.
Ответ: При
при
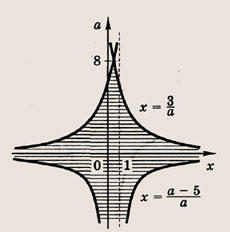
Задание 84.
Решение: Перепишем неравенства в виде
и штриховкой на координатной плоскости (х; а) отметим точки, координаты которых удовлетворяют этой системе неравенств
Записываем решение данной системы. Ответ: при
при
при
при
Задание 85.
Указание: Постройте графики
и (х + 1)2 + (у + 1)2=1 Ответ: {(-1; -2)} Задание 86.
Указание: Постройте графики функций
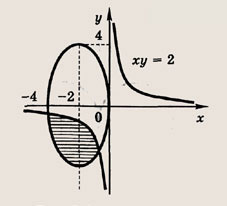
и у = 2х2 - 4х + 3 Ответ: 86. {(1; 1)}. Задание 87.
Решение: Запишем второе уравнение в виде
Это окружность радиуса
с центром (а; -а), лежащим на прямой у = -х
Пересечение с гиперболой
возможно только в том случае, если а = 0. При а = 0 получаем решения х1 = 1, у1 = 1 и х2 = -1, у2 = -1. Ответ: при
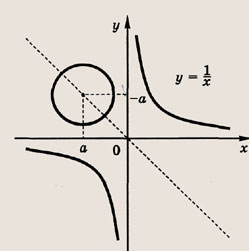
при других а решений нет. Задание 88. Прямая проходит через точку А(2; 1) и пересекает параболу у = х2 - 4х в точках, сумма квадратов абсцисс которых наименьшая. Запишите уравнение этой прямой.
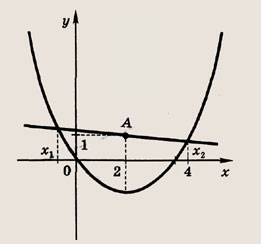
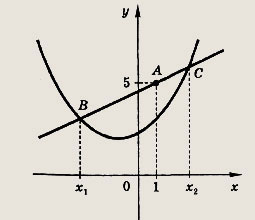
Запишем уравнение прямой в виде у = а(х - 2) + 1. Тогда точки пересечения этой прямой и параболы у = х2 - 4х
имеют абсциссы x1и х2, являющиеся корнями квадратного уравнения а(х - 2) + 1 = х2 - 4х, т. е. х2 - (а + 4)х + 2а - 1 = 0. Так как х12 + х22 = (x1 + х2)2 - 2х1х2 = (а + 4)2 - 2х1х2 = (а + 4)2 - 2(2а - 1) = а2 + 4а + 18 = (а + 2)2 + 14, то наименьшее значение сумма квадратов абсцисс принимает при а = -2. Ответ: у = -2х + 5 Задание 89. Прямая проходит через точку А(1; 5) и пересекает параболу у = х2 + х+1 в точках, сумма ординат которых наименьшая. Запишите уравнение этой прямой. Решение: Запишем уравнение прямой в виде у = а(х - 1) + 5. Тогда точки В и С пересечения этой прямой с параболой у = х2 + х + 1
имеют абсциссы x1 и х2, являющиеся корнями квадратного уравнения а(х - 1) + 5 = х2
+ х + 1, т. е. х2 - (а - 1)х + а - 4 = 0.
а сумма ординат точек пересечения равна
Следовательно, сумма ординат наименьшая при
Искомое уравнение имеет вид
Ответ:
Задание 90. Прямая проходит через точку Б(1; -3) и пересекает параболу у - 2х - х2 в точках, сумма ординат которых наибольшая. Запишите уравнение этой прямой. Ответ: -3 Задание 91. Найдите длину перпендикуляра, опущенного из точки А(3; -1) на прямую, пересекающую линию
и проходящую через точки этой линии с ординатами у = 1 и
Решение: Находим точки В и С пересечения прямой с кривой
Имеем
откуда х= 1, т.е. В (1; 1);
откуда х = 0, т. е.
Записываем уравнение прямой, проходящей через точки В и С:
т. е. х - Зу + 2 = 0. Уравнение перпендикуляра к этой прямой, проходящего через точку А (3; -1), имеет вид у = -Зх + 8. Теперь найдем координаты точки пересечения этих прямых, для чего решим систему уравнении:
откуда
Вычисляем расстояние между точками А(3;-1) и D
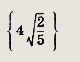
Имеем
Ответ: Задание 92. Найдите длину перпендикуляра, опущенного из точки А(5; 0) на касательную к параболе у = х2 + 3, проведенную из точки В(0; 1). Ответ:
Задание 93. На оси ординат найдите точку, через которую проходят две взаимно перпендикулярные касательные к графику функции у = х2 - 2х + 3. Решение: Уравнение касательной имеет вид у = ах + b
Приравнивая нулю дискриминант
квадратного уравнения получим D = (а + 2)2 - 4(3 - b) = 0, т. е. а2 + 4а + 4b - 8 = 0. Это уравнение должно иметь корни a1 и а2 такие, что а1а2 = -1 (а1 и а2 — угловые коэффициенты искомых касательных; записано условие перпендикулярности этих прямых). Но а1а2= 4b - 8, т. е. 4b -8 = -1, откуда
Ответ:
Задание 94. На прямой 2х - Зу = 6 найдите точку, через которую проходят две взаимно перпендикулярные касательные к графику функции
Указание: Запишите уравнения касательных в виде
Далее см. решение задачи 93. Ответ:
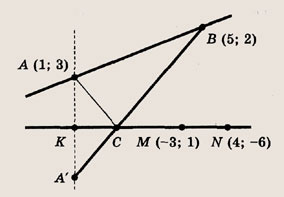
Задание 95. На координатной плоскости
даны точки А(1; 3) и В(5; 2). На прямой, проходящей через точки М(-3; 1) и Решение: Точка С
— это точка пересечения прямых (MN) и (А'В), где А' — точка, симметричная A относительно прямой (MN) (см. задачу 7). Подумайте, почему это так? Теперь последовательно находим: 1) уравнение прямой (MN):
T. e. х + у + 2 = 0; у - х -2=0; 3) координаты точки К, т. е. точки пересечения прямых (MN) и (АА):
откуда К(-2; 0);
откуда А'(-5; -3); 5) уравнение прямой (А'В):
т. е. 2у - х + 1 = 0;
откуда х = -1, у = -1 Ответ: С(-1; -1) Задание 96. Даны точка А(5; 7) и угол, уравнения сторон которого имеют вид у = 0 и у = х+5. Точки В и С лежат на разных сторонах угла. Найдите наименьшее значение периметра треугольника ABC. Указание: Наименьший периметр треугольника ABC равен длине отрезка PQ, где Р — точка, симметричная А относительно прямой у = 0, a Q — точка, симметричная А относительно прямой у = х + 5. Ответ:
Задание 97. Числа х, у и а удовлетворяют системе уравнений
Указание: Сначала выясните, при каких а данная система имеет решение. Эти значения
Далее из системы выразите произведение ху через а и найдите минимум полученной функции на отрезке
Ответ Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
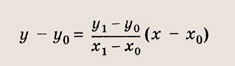
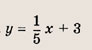
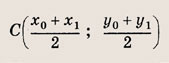
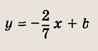
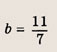
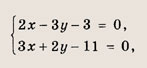
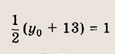
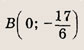
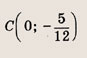
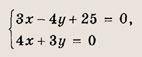
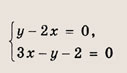
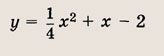
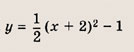
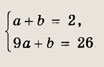
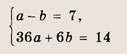
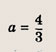
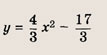
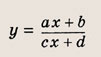
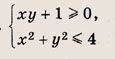
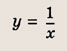
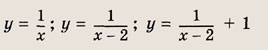
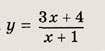
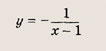
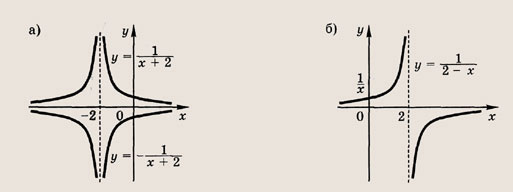
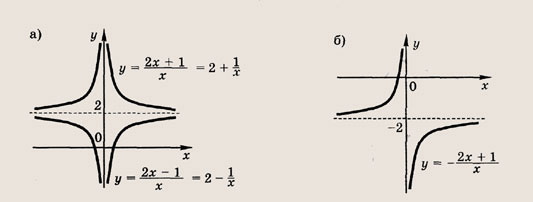
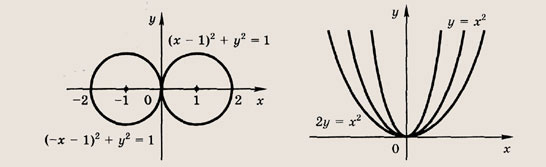
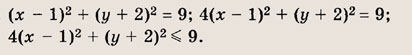
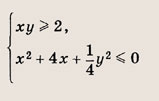
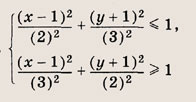
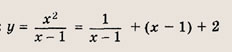
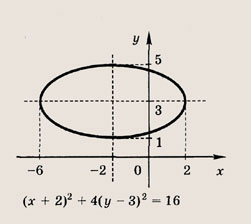
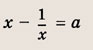
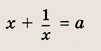
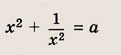
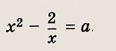
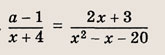
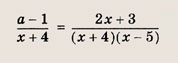
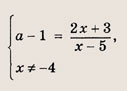
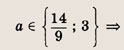
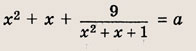
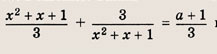
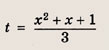
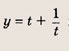
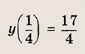
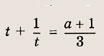
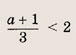
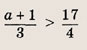
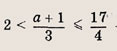
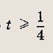
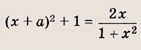
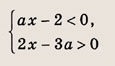
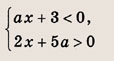
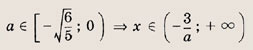
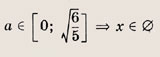
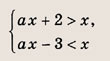
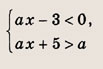
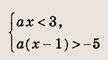
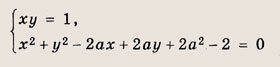
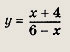
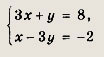
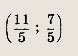
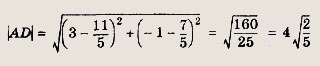
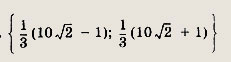
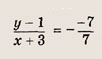

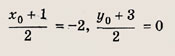
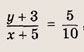
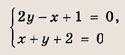
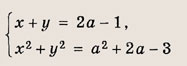
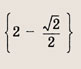
 Главная
Главная