Линейные и квадратичные
неравенства. Решение рациональных неравенств
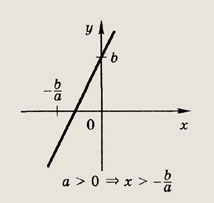
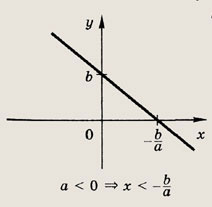
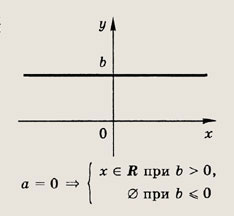
Выпишите самостоятельно
решения линейного неравенства при других знаках неравенства. Задание 1.
Ответ:
Задание 2.
Ответ:
Задание 3.
Ответ:
Задание 4.
Ответ:
Задание 5. (х + 2)2 + 8х2< (Зх -1)2 - 12 Ответ:
Задание 6.
Ответ:
Задание 7.
Ответ:
Задание 8.
Ответ: (2; 10] Задание 9.
Ответ: При
при
Задание 10.
Решение. Переписав систему в виде
откуда а > 1. Ответ: при
при
Задание 11.
Ответ:
Задание 12. |5 - 2х| > 3 Ответ:
Задание 13. |2х - 3| < х Указание: Здесь х > 0. Ответ: (1; 3) Задание 14. |х - 1| > х + 2 Решение: Если
то неравенство, очевидно,
выполнено. Если же х > -2, то х -1> х + 2 или х - 1 < -(х + 2), откуда
следует,
объединяя найденные решения, получаем ответ. Ответ:
Задание 15. Найдите все значения а, для каждого из которых числа л: и у, удовлетворяющие системе уравнений
удовлетворяют также неравенству х > у + 5а. Ответ:
где коэффициент
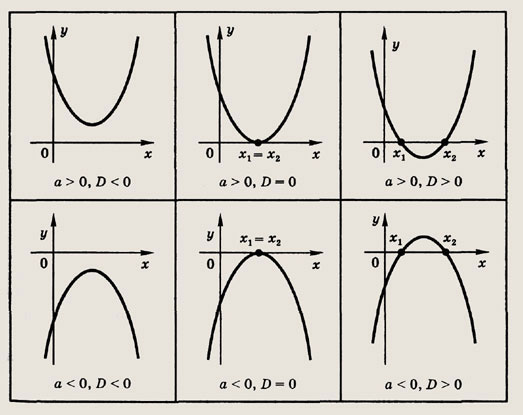
Решения всех этих неравенств получаем из следующей таблицы графиков квадратного трехчлена у = ах2 + bх + с.
Напомним, что здесь D = b2 - 4ас — дискриминант квадратного трехчлена у = ах2 + bх + с. В случае, когда D > 0, корни х1 и х2 квадратного трехчлена вычисляются по формулам
Решите следующие квадратичные неравенства и системы квадратичных неравенств (16—25): Задание 16.
Ответ:
Задание 17. 4 + Зх - х2 > 0 Ответ: (-1; 4) Задание 18.
Ответ:
Задание 19. (6х - 5)(х + 1) > (х + 2)(х + 3) Ответ:
Ответ:
Задание 21.
Ответ:
Задание 22.
Ответ:
Задание 23.
Ответ:
Задание 24. Зх4 + 7х2 - 10 < 0 Решение: Выполнив замену х2 = t, имеем 3t2 + 7t - 10 < 0, откуда
Решив систему неравенств
Ответ: ( -1; 1) Задание 25. 2х4 - Зх2 + 1 > 0 Ответ:
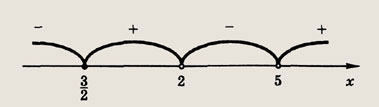
• Умение решать линейные и квадратичные неравенства является основой для решения общих рациональных неравенств методом интервалов, который состоит в следующем. Для решения неравенства
Методом интервалов решите следующие неравенства (26—36): Задание 26.
Ответ:
Задание 27.
Ответ:
Задание 28.
Ответ:
Задание 29.
Ответ:
Задание 30.
Указание: Квадратный трехчлен х2 + 2х + + 4 > 0 при всех х. Ответ:
Задание 31.
Ответ:
Задание 32.
Ответ:
Задание 33.
Ответ:
Задание 34.
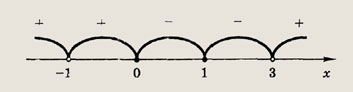
Решение: Раскладывая числитель и знаменатель дроби на множители, приходим к неравенству
Точки х = +2 в ответ не входят, так как это корни знаменателя дроби. Ответ:
Задание 35.
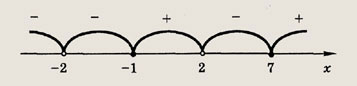
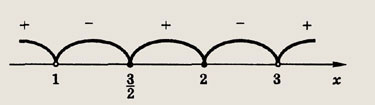
Указание: Воспользуйтесь тем, что х3 - 2х2 - 5х + 6 = (х + 2)(х - 1)(х - 3). Ответ:
Задание 36.
Ответ:
Решите следующие неравенства (37—50): Задание 37.
Ответ:
Задание 38.
Ответ:
Задание 39.
Решение: Выполним следующие преобразования:
Ответ:
Задание 40.
Ответ:
Задание 41.
Ответ:
Задание 42.
Ответ:
Задание 43.
Ответ:
Задание 44.
Решение: Переписав неравенство в виде
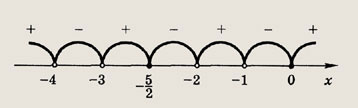
и приведя дроби к общему знаменателю, получаем неравенство
Его решение приведено на рис.
Ответ:
Задание 45.
Ответ:
Задание 46.
Решение: Так как х3 + 1 = (х + 1)(х2 - х + 1), то, записав неравенство в виде
Отсюда
Ответ:
Задание 47.
Ответ:
Задание 48.
Решение: Имеем
записываем ответ. Ответ:
Задание 49.
Ответ:
Задание 50.
Решение: Выполним следующие преобразования:
получаем ответ: Ответ:
Решите неравенства, которые сводятся к более простым квадратичным или рациональным неравенствам подходящей заменой переменной (51—58): Задание 51.
Указание: Выполните замену, полагая х2 + х + 1 = t. Ответ: (-2; 1) Задание 52.
Решение: Пусть х2 + 2х + 2 = t; тогда получим неравенство
Так как t = x2 + 2x + 2>0 при всех х, то неравенство равносильно следующему: 6(t + 1) - 6t < t(t + 1); t2 + t - 6 > 0, откуда t < -3 или t > 2. Первое из неравенств не имеет решении, а второе приводит к неравенству х2 + 2х > 0, откуда
Ответ:
Задание 53. x8 - 6х7 + 9х6 - х2 + 6х - 9 > 0 Указание: х8 - 6х7 + 9х6 - х2 + 6x - 9 = (х6 - 1)(х2 -6х + 9) = (х- 3)2(х - 1)(х + 1)(х4 + х2 + 1). Ответ:
Задание 54.
Указание: х4 + 4х3 + 4х2 - 9 = (х2 + 2х)2 - 9. Ответ:
Задание 55.
Указание: Положите
Ответ:
Задание 56.
Решение: Отметим, что х = 0 является решением данного неравенства. Если же
то перепишем его в виде
второго:
а третьего:
Объединяя решения неравенств и добавляя точку х = 0, получаем, что
Ответ:
Задание 57. Зх3 - 14х2 + 20х > 8 Указание: Зх3 - 14х2 - 20х - 8 = (3х - 2)(х - 2)2. Ответ:
Задание 58.
Решение: Имеем
Ответ: х € (0; 1] U [2; 3] Решите следующие неравенства, содержащие знак модуля величины (59—76). Задание 59. х2 - 5|х| + 6 > 0 Ответ:
Задание 60.
Решение: Раскладывая квадратный трехчлен на множители, получаем
Ответ: Задание 61. |х - 1 + |х + 1| < 4 Решение: Рассмотрим следующие случаи: 1)
2)
3)
Объединяя найденные решения, получаем решение неравенства. Ответ: х € (-2; 2) Задание 62. |1 + 2х| -|х + 2| < 2 Ответ:
Задание 63.
Решение: Данное неравенство равносильно совокупности следующих неравенств:
Решение первого из них -
Объединяя эти решения, получаем решение исходного неравенства. Ответ:
Задание 64.
Указание: Неравенство равносильно системе неравенств:
Ответ:
Задание 65.
Ответ:
Задание 66.
Ответ:
Задание 67.
Решение: Это неравенство имеет вид
что возможно только в том случае, если
(получается равенство). Таким образом, исходное неравенство равносильно следующему.
т. е.
откуда
Ответ:
Задание 68. ||х2 + 5х| - 6| > |х2 + 5х| - 6 Ответ:
Указание: Данное неравенство равносильно неравенству |х2 + 5х| - 6 < 0. Задание 69. ||х - 1| > |х| Ответ:
Задание 70. |2 - |х|| < 2|х| Ответ: Задание 71.
Решение: Рассмотрим следующие случаи: 1)
Ответ:
Задание 72.
Ответ:
Задание 73. ||х2 - 3х + 2| - 1 > х - 2 Ответ:
Задание 74. |х2 -2х - 3| + 2|х- 2| < 5 Ответ:
Задание 75. |12x2 + 33x + 32| < |4x2 + 35x + 38| Ответ:
Задание 76.
Ответ:
Установите, при каких а следующие неравенства выполняются для всех
(77—81): Задание 77. x2 -2(а -1)x + а + 5 > 0 Указание: Поскольку коэффициент при х2 положителен, нужное значение а определяется условием D < 0. Ответ: (-1; 4) Задание 78. (а2 - 1I)x2 + 2(а - 1)x + 2 > 0 Ответ:
Задание 79.
Решение: Так как х - х2 - 1 < 0 для всех х, то исходное неравенство можно умножить на (х - х2 - 1), при этом знак неравенства изменится на противоположный:
Последнее неравенство выполняется для всех х, если
Ответ: [-1; 7] Задание 80.
Ответ: Задание 81.
Ответ: (-1; 5) Задание 82. Найдите все а, при которых неравенство ах2 - 4х + За + 1 > 0 выполнено для всех х > 0. Решение: Положим f(x) = ах2 - 4х + За + 1. Данное выражение положительно при всех х > 0 в двух случаях
Последнее неравенство второй системы означает, что абсцисса вершины параболы отрицательна. Так как в этой системе первое и четвертое неравенства несовместны, то искомые значения а удовлетворяют первой системе:
Ответ:
Задание 83. Найдите все а, при которых неравенство х2 + ах + а2 + 6а < 0 выполнено для всех х € (1; 2). Указание: Для нахождения требуемых значений а достаточно решить систему
Ответ:
Задание 84. При каких т все решения неравенства (m - 1)х2 + (m2 - 2m + 2)х +m - 1 > 0 положительны и меньше 2? Решение: Найдем корни уравнения (m - 1)х2 +
(m2 - 2m + 2)х + m - 1 = 0.
Ответ:
Задание 85. Найдите все а, при которых неравенство
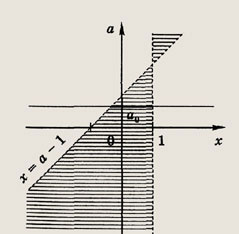
Решение: На плоскости хОа изобразим множество пар (х; у), для которых выполняется требуемое неравенство
Искомые значения а0 характеризуются тем, что отрезок прямой а = а0 при
полностью лежит в заштрихованной области. Это достигается при
Ответ:
Задание 86. Найдите все а, при которых неравенство
Решение: Данное неравенство должно, в частности, выполняться при х = 0. В этом случае оно имеет вид
откуда
выражение х + 6 > 0. Таким образом, при указанных ограничениях исходное неравенство имеет вид
и неравенство выполняется при всех х € (-1; 1), если оно выполняется при х = 1, т. е.
получим ответ. Ответ:
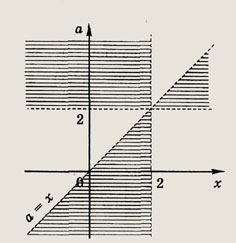
Задание 87. При каких а неравенство х2 + |х + а| < 2 имеет хотя бы одно положительное решение? Решение: На плоскости хОа изобразим множество точек, координаты которых удовлетворяют неравенству х2 + |х + а| < 2.
При
неравенство имеет вид а < 2 - х - х2; при х + а < 0 — вид а >х2- х - 2.В заштрихованной области точки с положительной абсциссой существуют при
Ответ:
Задание 88. При каких а неравенство х2< 4 - |х - а| имеет хотя бы одно отрицательное решение? Ответ:
Задание 89. При каких а имеет единственное решение система неравенств:
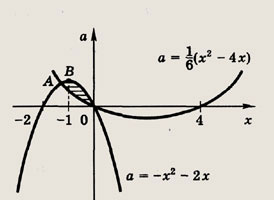
Решение а). На плоскости хОа изобразим параболы а = -х2 - 2х и
Точки, координаты которых удовлетворяют данной системе, лежат ниже параболы а = -х2 - 2х и выше параболы
Эти параболы пересекаются в точках О(0; 0) и
Заметим, что точка А расположена левее вершины первой параболы В(-1; 1). Горизонтальная прямая пересекает заштрихованную область по единственной точке, если она проходит через точки О и В, т. е. при а = 0 и а = 1. Ответ: {0; 1}. б) {0; -1} Задание 90. Найдите все а, при которых существует хотя бы одно общее решение неравенств:
Ответ: Задание 91. Найдите все а, при которых любое число х € R является решением хотя бы одного из неравенств:
Ответ:
Задание 92. Найдите все а, при которых любое решение неравенства
является также решением неравенства х2 + 2х - 1 + а2 > 0. Ответ:
Решите следующие неравенства и системы неравенств (93—104): Задание 93.
Решение: Умножив левую и правую части неравенства на 6 и приведя подобные члены, получаем х (а2 - 9) < а + 3. Рассмотрим следующие случаи: 1) при а < -3 выражение (а2 - 9) > 0, поэтому
3) при -3 < а < 3 выражение (а2 - 9) < 0 , поэтому
5) при а > 3 имеем (а2 - 9) > 0 и, значит,
Ответ: при
при
при
Задание 94. х2 - ах + а - 1 < 0 Решение: Запишем неравенство в виде (х — (а — 1))(х - 1) < О и изобразим точки, координаты которых удовлетворяют ему по плоскости хОа.
При фиксированном а0 решения — это абсциссы точек прямой а = а0, попавшие в заштрихованную область. Ответ: при
при а = 2 => 0; при
Задание 95. ах2 - (а + 4)х + 4 > 0 Указание:
Ответ:
при
при
Задание 96.
Ответ: При
при
Задание 97.
Решение: Приведем неравенство к виду
и заштрихуем на плоскости хОа множество точек, координаты которых ему удовлетворяют.
Ответ: при
при
при
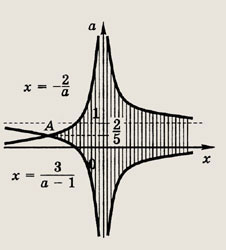
Задание 98.
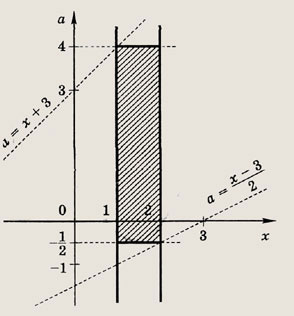
Решение: На плоскости Оха изобразим множество точек, удовлетворяющих неравенствам: ах > -2, ах < х + 3
Для нахождения ординаты точки А приравняем правые части уравнений
и
Получаем
Ответ: при
при
Задание 99.
Ответ: При
при
при
Задание 100.
Ответ:
при
при
при
при
при
Задание 101. |х + За - 6| < |3х - 2 + 7а| Решение: Так как
Ответ: при
Задание 102.
Решение: На плоскости изобразим Оха
множество точек, удовлетворяющих данному неравенству.
Ответ: npи
при
при
при
Задание 103.
Ответ: При
при
при
при
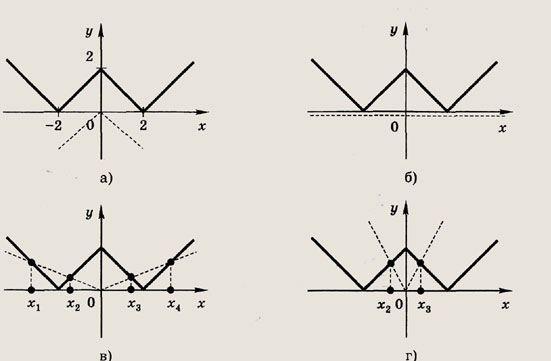
Задание 104. ||х - 2| > 2а|x| Решение: Здесь требуется найти те значения переменной х, при которых график функции у = ||х| - 2| лежит выше графика у = 2а\х\. Первый график не зависит от параметра, а второй меняется при изменении а. Рассмотрим различные случаи: 1) а < 0 (рис. а). Условию удовлетворяют все
2) а = 0 (рис. б). Условию задачи удовлетворяют
3)
(рис. в).
Найдем координаты точек пересечения графиков:
Условию удовлетворяют
4)
(рис. г). Условию удовлетворяют
Ответ: при
при
при
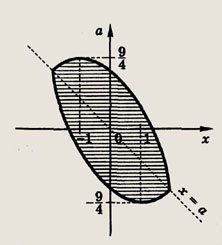
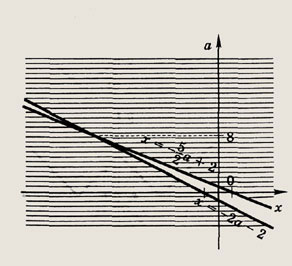
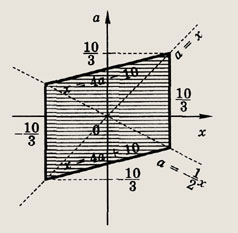
Задание 105. При каких а фигура, задаваемая неравенствами
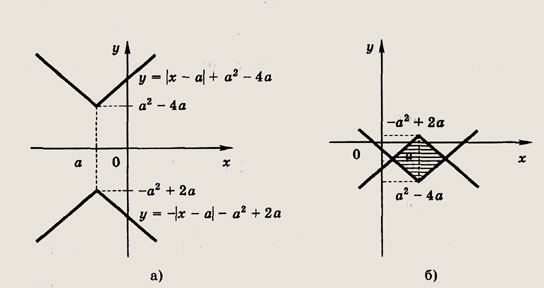
имеет наибольшую площадь? Найдите эту площадь. Решение: На плоскости хОу изобразим множество точек, удовлетворяющих данной системе неравенств.
В первом случае соответствующие области не имеют общих точек, а во втором общие точки лежат внутри заштрихованного квадрата. Второй случай имеет место, если
Диагональ заштрихованного квадрата равна 6а - 2а2, т. е. его площадь
Наибольшее значение функции S(a) на [0; 3] достигается при
так как при
Ответ:
Задание 106. При каких а фигура, задаваемая неравенствами
имеет наименьшую площадь? Найдите эту площадь. Ответ:
Задание 107. Из города А в город В, находящийся в 240 км от А, со скоростью 40 км/ч выходит автобус. Одновременно с ним из Б в A с постоянной скоростью v (км/ч) выезжает автомобиль. Через полчаса после встречи автомобиль, не доезжая до города А, поворачивает обратно и с прежней скоростью движется по направлению к В. Найдите все те значения и, при которых автомобиль приходит в В раньше, чем автобус. Решение: Время, которое автомобиль и автобус затратили до их встречи, составляет
Автобус доезжает до В за 6 ч, а автомобиль находился в пути
Получаем
Это расстояние больше, чем
откуда
Ответ: (56; 120) Задание 108. От пристани А к пристани В, находящейся от А на расстоянии 12 км, вниз по течению отходит моторная лодка, скорость которой в стоячей воде равна 6 км/ч. Одновременно с ней из Б в А выходит катер, скорость которого в стоячей воде равна 10 км/ч. После встречи они разворачиваются и возвращаются на свои пристани. Определите все значения v, при которых моторная лодка приходит в А не раньше, чем через 1 ч после возвращения катера в Б, если v — скорость течения. Ответ: (2; 6) Задание 109. Некоторое предприятие приносит убытки, составляющие 31 тыс. р. в год. Для превращения его в рентабельное было предложено увеличить ассортимент продукции. Подсчеты показали, что дополнительные доходы, приходящиеся на каждый новый вид продукции, составят 25 тыс. р. в год, а дополнительные расходы окажутся равными 5 тыс. р. в год при освоении одного нового вида, но освоение каждого последующего потребует на 10 тыс. р. в год больше расходов, чем освоение предыдущего. Можно ли указанным способом сделать предприятие рентабельным? Ответ: Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
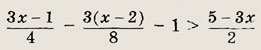
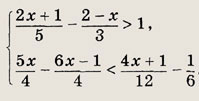
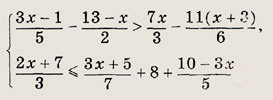
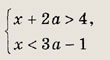
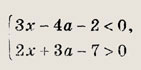


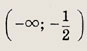
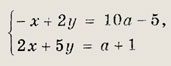
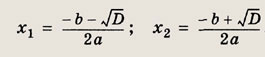
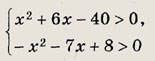
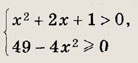
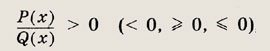
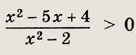
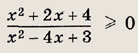
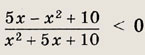
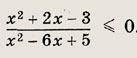
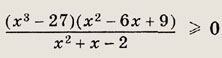

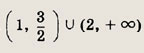
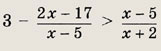
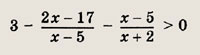
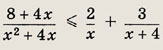
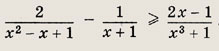
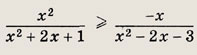
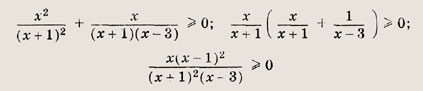
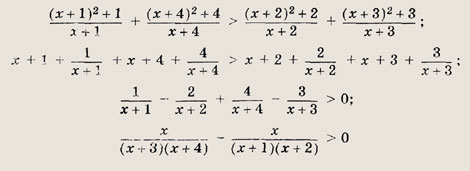
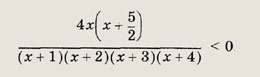
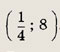
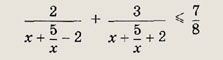

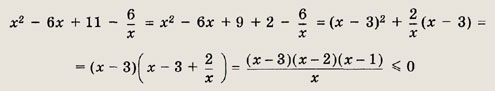

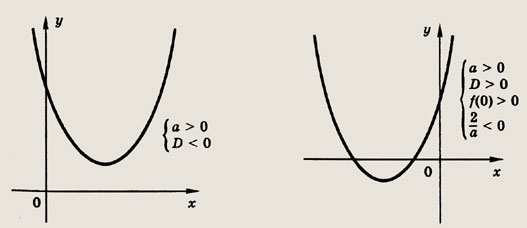
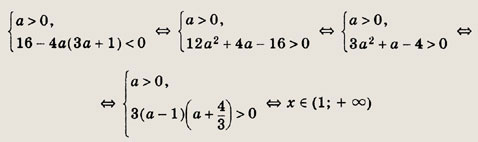
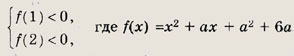
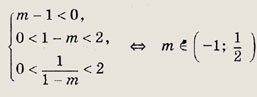
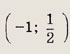
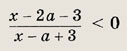
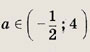

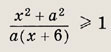

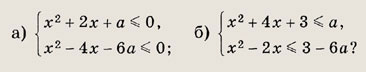
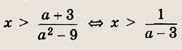
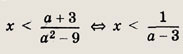
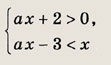
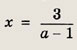
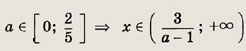
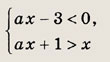
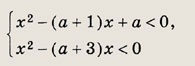

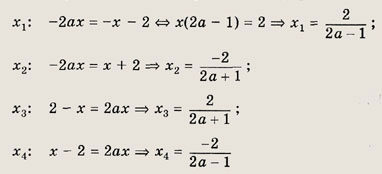
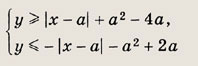
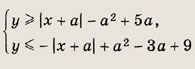
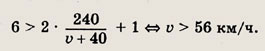
 Главная
Главная