Иррациональные уравнения и неравенства
При решении простейших
иррациональных уравнений придерживайтесь следующих схем.
в данном случае не нужно. Уравнение
f(x) = g3(x). Решите простейшие и сводящиеся к простейшим уравнения (1—22): Задание 1.
Решение: Данное уравнение равносильно системе
Решаем последнее уравнение; имеем х2 - Зх + 2 = 0, откуда х1 = 1; Х2 = 2. Оба решения удовлетворяют неравенству х + 1 > 0. Ответ: {1; 2} Задание 2.
Ответ: 2 Задание 3.
Ответ: 2 Задание 4.
Ответ:
Задание 5.
Ответ: 2 Задание 6.
Ответ: 23 Задание 7.
Ответ: 0 Задание 8.
Решение: Уравнение равносильно следующему: 9 - х = (3 - х)3, т.е. х3 - 9х2 + 26х - 18 = 0 Одним из решений этого
уравнения является х = 1. Разделив х3 -- 9х2 + 26х - 18
на (х - 1), получим Так как уравнение х2 - 8х + 18 = 0 не имеет действительных корней, то единственное решение исходного уравнения — это х = 1. Ответ: 1 Задание 9.
Ответ: 3 Задание 10.
Ответ: Задание 11.
Ответ:
Задание 12.
Ответ:
Задание 13.
Решение: Отметив, что х # 1, преобразуем уравнение к виду
Последнее уравнение равносильно системе
Ответ: -2 Задание 14.
Ответ: 26 Задание 15.
Ответ: 1 Задание 16.
Ответ:
Задание 17.
Ответ: 2 Задание 18.
Ответ:
Задание 19.
Ответ: {0; 2} Задание 20.
Заметив, что х # -1, преобразуем уравнение к виду
Выражение х2 + х + 1 > 0 при любых действительных х. Поэтому последнее уравнение равносильно следующему: 1 - х3 = (х2 + х + 1)2. Но 1 - х3 = (1 - х)(1 + х + х2), а х2 + х + 1 > 0, поэтому приходим к уравнению 1 - х = х2 + х + 1, х2 + 2х = 0, откуда х1 = 0; х2 = -2. Ответ: (-2; 0} Задание 21.
Ответ:
Задание 22.
Решение: Умножим числитель и знаменатель каждой из дробей на сопряженное выражение. Тогда уравнение преобразуется к виду
Последнее уравнение равносильно системе
откуда х = 4. Ответ: 4
Решите уравнения (23—32), сводя их к простейшим подходящей заменой: Задание 23.
Ответ: -6 Задание 24.
Ответ: 5/2 Задание 25.
Ответ: {-5, 6} Задание 26.
Указание: Полагая
упростите полученные дроби. Ответ:
Задание 27.
Решение: Полагая
сведем уравнение к квадратному относительно у: 4у = 12 - у2, т.е. у2 + 4у - 12 = 0. Отсюда у1 =2; у2 = -6 (постороннее решение, так как
Поэтому исходное уравнение равносильно уравнению
откуда х1 + Зх - 6 = 4; х1 + Зх - 10 = 0. Следовательно, х1 = -5; х2 = 2. Ответ: {-5; 2} Задание 28.
Ответ:
Задание 29.
Ответ: {-3;6} Задание 30.
Ответ: {-7; 2} Задание 31.
Ответ:
Задание 32.
Ответ:
Задание 33.
Решение: Уравнение равносильно системе Решив уравнениех2 - 6х + 5 = 0, получаем х1 = 1 (не удовлетворяет первому неравенству), х2 = 5. Ответ: 5 Задание 34.
Ответ: 2 Задание 35.
Ответ:
Задание 36.
Ответ:
• Если уравнение содержит два или более радикала, то по возможности рекомендуется придерживаться следующих правил: 1) указать область определения данного уравнения; 2) распределить радикалы по обеим частям уравнения так, чтобы обе части стали неотрицательными; 3) только после этого возводить в квадрат правую и левую части уравнения.
Задание 37.
Решение: Найдем область определения данного уравнения:
Перенесем
в правую часть равенства, после чего обе части равенства станут неотрицательными. Получаем равносильную систему
28 Задание 38.
Ответ: {2; 34} Задание 39.
Ответ: 2 Задание 40.
Ответ: 0 Задание 41.
Решение: Перепишем уравнение в виде
Возводим в квадрат обе части равенства:
откуда
Последнее уравнение равносильно системе
Ответ: -9 Задание 42.
Ответ: 6 Задание 43.
Ответ: 6 Задание 44.
Ответ:
Задание 45.
Решение: Область определения данного уравнения состоит из всех значений переменной х, удовлетворяющих неравенству
(проверьте!). Переписав уравнение в виде
возведем обе части в квадрат и получим:
Отсюда
Это уравнение равносильно системе
Тогда
Ответ: 8 Задание 46.
Ответ: 5 Задание 47.
Решение: Уравнение сводится к простейшему иррациональному уравнению умножением обеих частей равенства на
При этом возможно появление посторонних решений. Поэтому необходимо сразу указать область допустимых значений переменной х. Получаем
равносильно исходному. Решив это уравнение, находим
Ответ: -3 Задание 48.
Ответ:
Задание 49.
Ответ:
Задание 50.
Решение: Область допустимых значений
При этих х исходное уравнение равносильно следующему:
Возведя в квадрат обе части равенства, приходим к уравнению
Теперь при
снова возведя в квадрат, получаем 16х2 = 68. Решение
удовлетворяет неравенству
Ответ:
Задание 51.
Решение: Заменой у = 2х2 - Зх уравнение сводится к виду
Решив его, получаем у = -1. Отсюда 2х2 - Зх = -1, т. е. 2х2 - Зх + 1 = 0. Ответ:
Задание 52.
Ответ:
Задание 53.
Решение: Этот пример значительно труднее предыдущих. Введем новую переменную
Заметим, что у > 0 при всех допустимых х € [2; 4]. Теперь имеем
Отсюда при
получаем
а само исходное уравнение примет вид
у2(у2 - 4) + 4(у - 2) - У2(у + 2)(у- 2) + 4(у - 2) = (у -2)[у2(у + 2)+ 4] = 0. Поскольку
единственным решением этого уравнения является значение у = 2. Таким образом, исходное уравнение равносильно уравнению
решив которое, находим х = 3. Ответ: 3 Задание 54.
Указание: Положите
Далее см. решение задачи 53 в предыдущем задании. Ответ: {1, 5}.
Задание 55.
Решение: Запишем уравнение в виде
Поэтому область допустимых значений, с учетом неравенства
состоит только из тех х, для которых выполнено условие
и точки х = -1. Проверяем,
что х = -1 — решение исходного уравнения.
приходим к равносильному при
уравнению:
Ответ: {-1; 1} Задание 56.
Решение: Перепишем уравнение в виде
Ответ: {-1; 0; 1} Задание 57.
Ответ:
Задание 58.
Ответ:
Задание 59.
Решение: При
справедливо неравенство
монотонно возрастающая. Поэтому удобнее решать уравнение так:
Ответ: -3 Задание 60.
Ответ: -1 Задание 61.
Ответ: {-2; 0} Задание 62.
Решение: Сделаем замену у = х2 + х + 1. Получим уравнение
Решив его, находим у = -4 и у = 1. Уравнение х2 + х + 1 = -4 не имеет решений, а х2 + х + 1 = 1, т. е. х2 + х = 0, имеет решения x1 = -1; х2 - 0. Ответ: {-1, 0} Задание 63.
Решение: Перепишем уравнение в виде
это уравнение равносильно следующему:
откуда
Снова возводя в квадрат обе части равенства и раскрывая скобки, приходим к уравнению 6х2 + 7х + 1 = 0, откуда
Оба решения входят в область допустимых значений. Ответ:
Задание 64.
Ответ:
Задание 65.
Решение: Сделаем замену
Возводя в квадрат, получаем
Тогда исходное уравнение запишется в виде у = у2 - 20, у2 - у - 20 = 0, откуда у1 = 5; у2 = -4 (постороннее решение, так как
Теперь, решив уравнение:
получаем х = 3. Ответ: 3 Задание 66.
Ответ: 1 Задание 67.
Указание: Смотри решение задачи 68. Ответ: {-6; 1} Задание 68.
Решение: Умножим обе части равенства на сопряженное к левой части выражение, т. е. на
Получим
Решаем это уравнение, сводя его к алгебраической системе (см. далее задачи 71—80). Положим
Тогда величины а и b являются решениями системы
Заметим, что значения переменной а можно не находить. Решив два простейших уравнения,
получаем корни х1 = 4; x2 = -3. Ответ: {-3; 4} Задание 69.
Решение: В области определения данного уравнения, т. е. при
- оно равносильно следующему:
получаем
при всех допустимых значениях переменной х. Следовательно, последнее уравнение равносильно системе
а уравнение преобразуется к виду
Решаем это уравнение и получаем x1 = 3; х2 = - 7. Решение х = 3 — постороннее, поскольку должно быть
Ответ: 7 Задание 70.
Решение: Перенося
в правую часть уравнения, получаем
При всех допустимых значениях
правая часть уравнения неотрицательна, так как
при этих значениях х. Но тогда равенство имеет смысл лишь при
При х € [0; 3] исходное уравнение равносильно следующему:
откуда
Теперь легко видеть, что
Решая его, получаем
Второе решение постороннее, так как х € [0; 3]. Ответ:
Задание 71.
Решение: Полагая
приходим к системе
откуда
Теперь решаем уравнения Получаем x1 = -3; х2 = 3. Ответ: {-3; 3) Задание 72.
Ответ: 9 Задание 73.
Ответ: 0 Задание 74.
Ответ: 2401 Задание 75.
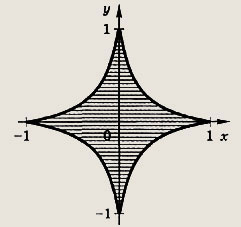
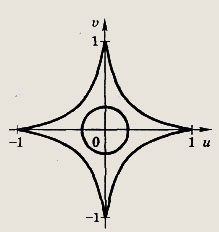
Решение: Полагая
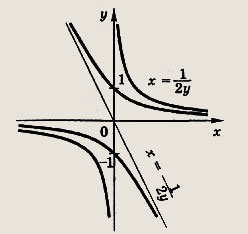
получаем систему уравнений
Ответ: 1; 2; 10 Задание 76.
Ответ: {-88; -24; 3} Задание 77.
Решение: Полагая
приходим к системе уравнений
b4 + 8b3 + 24b2 + 32b + 16 = 16. Получаем b(b3 + 8b2 + 24b + 32) = 0. Отсюда b = 0, а так как
то уравнение b3 + 8b2 + 24b + 32 = 0 решений не имеет. Итак,
откуда х = 8. Ответ: 8 Задание 78.
Ответ: {-79; 1} Задание 79.
Решение: Положим
Тогда
а2 - За + 2 = 0, т.е. а = 1; а = 2. Решив уравнения
находим х= -2, х = 5. Ответ: {-2; 5} Задание 80.
Положим
Тогда а2 + b2 = 2х + 2, откуда 4 - 2х = 6 - а2 - b2. Поэтому можно записать систему
Решив первое уравнение, получаем, что a + b = 2 или a + b = -3. Второе равенство невозможно, поскольку
Таким образом,
Ответ: 1 Примечание: Сравните решения задач 79, 80, полученные сведением к системе уравнений, с решениями задач того же типа (65—68) другим методом.
Задание 81.
Ответ:
Задание 82.
Решение: Перепишем уравнение в виде
Рассмотрим следующие случаи: 1)
что невозможно; 2)
т. е. в этом случае, при
уравнение выполняется тождественно; 3)
что невозможно. Ответ: х € [0; 3]
Ответ: (1; 26} Задание 84.
Ответ: 15 Задание 85.
Решение: Рассмотрим два случая: 1)
откуда х1 = -1; х2 = 23 (посторонний корень); 2)
откуда x1 = -1; x2 = 7. Ответ: {-1; 7} Задание 86.
Ответ: -1 Задание 87.
Ответ:
Задание 88.
Решение: Рассмотрим следующие случаи: 1)
что невозможно; 2)
откуда следует, что
Это также невозможно, поскольку должно быть х > -2. 3)
откуда при
4)
т.е. 3х=3х. Таким образом, любое число
удовлетворяет уравнению. Ответ:
Задание 89.
Решение: Полагая
сведем исходную систему к виду
Тогда
т. е. х = 11, у = 34. Ответ: (11; 34) Задание 90.
Ответ:
Ответ: {(17; -10); (17; 10)} Задание 92.
Указание: Подставьте у = 1 - х в первое уравнение системы. Ответ: (2; -1) Задание 93.
Ответ: (4; 16) Задание 94.
Ответ: {(5; 4); (-9; 25)} Задание 95.
Ответ:
Задание 96.
Решение: Положим
Тогда
Последняя система не имеет решений, так как должно быть
Получаем u = 1, v = 2 или v = 1, u = 2. Отсюда х = 1; у = 1 или х = -2; у = 4. Ответ: {(1; 1); (-2; 4)} Задание 97.
Решение: Положим
Тогда
Теперь исходная система примет вид
(2; 2) Задание 98.
Указание: Перемножьте уравнения системы. Ответ: (5; 4) Задание 99.
Решение: Здесь следует рассмотреть два случая. 1) Пусть х + у > 0. Тогда и
Умножая обе части равенства на (х + у), приходим к уравнению
получаем
Далее решаем систему
Отсюда
так как из неравенств следует, что
2) Пусть х + у < 0. Тогда и
При этом справедливо равенство Снова полагая
теперь приходим к системе
Ответ:
Задание 100.
Ответ: Задание 101.
Решение: Из первого уравнения системы следует, что
а второе определено лишь при
Значит, z = 1. Тогда первое уравнение дает х - у = 0. Следовательно, х = у = 4. Ответ: (4; 4; 1)
• Простейшее иррациональное неравенство вида
равносильно совокупности следующих двух систем: а неравенство вида
равносильно системе неравенств
переходит в равносильное после возведения в куб обеих его частей.
Задание 102.
Ответ: (3; 4] Задание 103.
Ответ:
Задание 104.
Ответ:
Задание 105.
Решение: Неравенство равносильно совокупности двух систем:
Ответ:
Задание 106.
Ответ:
Задание 107.
Ответ:
Задание 108.
Ответ:
Задание 109.
Решение: Неравенство равносильно системе
Решив ее, получаем
Ответ:
Задание 110.
Ответ:
Задание 111.
Ответ:
Задание 112.
Ответ:
Задание 113.
Решение: Неравенство равносильно совокупности систем:
Задание 114.
Ответ: [-2; -1) U (0; 1] Задание 115.
Решение: Рассмотрим два случая. 1) Пусть х > 1. Тогда неравенство равносильно следующему:
Учитывая, что х > 1, находим решение х € (1; 2]. 2) Пусть теперь х < 1. Тогда
Решив это неравенство, получаем х € [-1; 0]. Ответ: х € [-1; 0] U (1; 2] Задание 116.
Ответ:
Задание 117.
Ответ:
Задание 118. Указание: Запишите неравенство в виде
Теперь оно равносильно совокупности
Ответ:
равносильны: Задание 119.
Ответ:
Задание 120.
Ответ:
Задание 121.
Ответ:
Задание 122.
Ответ:
Задание 123.
Ответ: [-5; -1] Задание 124.
Ответ: [ -1; 1]
Решение: Заметив, что
(это область допустимых значений), возводим обе части неравенства в квадрат. Получаем
откуда
Значит, исходное неравенство равносильно следующей системе:
Ответ:
Задание 126.
Ответ: [-3; 1] Задание 127.
Ответ:
Задание 128.
Решение: Найдя область допустимых значений х € [6; 10], перепишем неравенство в виде
Теперь, возводя в квадрат, получаем
Следовательно, исходное неравенство равносильно системе
Решив его, получаем
Ответ:
Задание 129.
Ответ:
Задание 130.
Ответ:
Задание 131.
Решение: Указав область допустимых значений
и переписав неравенство в виде
возводим его обе части в квадрат. Имеем
получаем
Ответ:
Задание 132.
Ответ:
Задание 133.
Ответ:
Задание 134.
Ответ: [0; 16] Задание 135.
Ответ:
Задание 136.
Ответ:
Задание 137.
Решение: Сделав замену х2 - 2х - 2 = t и учитывая, что
получим
возводя это неравенство в квадрат, находим t € [0; 1). Таким образом, исходное неравенство равносильно системе квадратичных неравенств
откуда
Задание 138.
Решение: Сразу запишем область допустимых значений: х € [3; 5]. Сделаем замену, полагая
Тогда
Теперь исходное неравенство перепишется в виде
Получаем систему неравенств Легко видеть, что ее первое неравенство выполняется при всех допустимых значениях х € [3; 5]. Решаем второе неравенство. Оно приводит к двум системам:
Ответ:
Задание 139.
Ответ:
Задание 140.
Ответ:
Задание 141.
Ответ:
Задание 142.
Ответ:
Задание 143.
Решение: Учитывая, что х > -1 и полагая
2у < у2 - 3, т. е. у2 - 2у - 3 > 0. Отсюда у > 3. Теперь решим неравенство
Возведя в квадрат и учитывая, что х > - 1, получаем решение:
Задание 144.
Ответ:
Задание 145.
Решение: Область допустимых значений есть
При этих х получаем
приходим к неравенству
Имеем
получаем х € [3; 4]. Ответ: [3; 4]
Решите неравенства (146—149), начав с отыскания области допустимых значений: Задание 146.
Ответ:
Задание 147.
Ответ:
Задание 148.
Решение: Находим область допустимых значений:
Если х € [-3; 0), то правая часть неравенства отрицательна, т. е. при этих значениях х неравенство не выполняется. Рассматриваем далее
В этом случае обе части неравенства неотрицательные. Возведя неравенство в квадрат, получаем
за исключением корней уравнения
Корень
принадлежит промежутку
и должен быть исключен. Итак,
Ответ:
Задание 149.
Ответ:
Задание 150.
Решение: Учитывая, что
при любом
а
перепишем неравенство в виде
Рассмотрим два случая. 1) Если
то получаем
Следовательно, неравенство справедливо при любом х € [0; 9). б) Если
то получаем
неравенство, находим:
Ответ:
Задание 151.
Ответ:
Задание 152.
Ответ:
Задание 153.
Решение: Имеем
Поэтому неравенство перепишется в виде
то, раскрывая модуль, получаем
что невозможно. Если же
Следовательно, Ответ:
Задание 154.
Ответ:
Задание 155.
Ответ:
Задание 156.
Ответ:
Задание 157.
Ответ:
Задание 158. Проверьте, что каждое решение неравенства
удовлетворяет также неравенству
Решение: Положим
Тогда следует проверить, что если величины а и b удовлетворяют неравенству а + b > 2, то
т. е. а2 + b2> 2. Но
а, следовательно,
Решите следующие уравнения и неравенства, содержащие параметры (159—173): Задание 159.
Ответ: при
при
Задание 160.
Ответ:
при
при
Задание 161.
Решение: Уравнение равносильно системе
Первый корень при всех допустимых значениях а, т. е. при
удовлетворяет неравенству
Для второго корня получаем
Ответ: при
при
при
Задание 162.
Ответ: при
при
Задание 163.
Решение: Уравнение равносильно следующей системе: Решив квадратное уравнение, получаем
при всех допустимых значениях а, т. е. при
Для второго корня это неравенство приводит к условию
Ответ: при
Задание 164.
Ответ: при
при
Задание 165.
Ответ: при
при
Задание 166.
Решение: Неравенство равносильно совокупности двух систем:
при
Ответ: при
при
Задание 167.
Решение: Неравенство равносильно следующей системе:
Ответ: при
при
Задание 168.
Ответ: при
при
Задание 169.
Ответ: при
при
Задание 170.
Ответ:
при
Задание 171.
Решение: Неравенство равносильно совокупности систем:
Выполнив преобразования, получаем
Если же
Ответ: при
при Задание 172.
Решение: Неравенство равносильно совокупности двух систем:
Мы видим, что решения первой системы записываются следующим образом: при
Аналогично решаем вторую
систему. Корни уравнения 2х2 - 4ах + а2 = 0
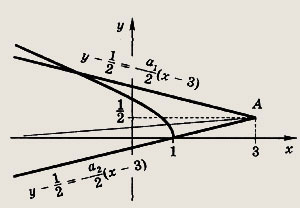
В зависимости от знака а теперь расположение корней на числовой оси изображено на рис.
Ответ:
Задание 173.
Решение: Область допустимых значений неравенства есть
Отсюда следует, что
Значение a = 0 приводит к пустому множеству решений. Рассмотрим далее значения а > 0. Возведя в квадрат, получаем
откуда при а € (0; 2] => х € [-а; а]. Если
то, снова возведя неравенство в квадрат, имеем 4х2< а3(4 - а), откуда при
а при
Объединяя полученные решения, записываем ответ. Ответ: при
при а € (0;2) => х €
[-a;a]
Задание 174. Найдите все а, при которых решения уравнения
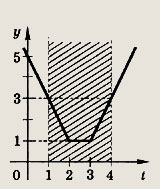
Ответ: а € [1; 5] Задание 175. Найдите все а, при которых решения уравнения
существуют и принадлежат отрезку [2; 17]. Решение: Преобразовав уравнение к виду
и введя новую переменную
переформулируем условие задачи следующим образом: найти такие а, при которых решения уравнения |t - 2| + |t - 3| = а существуют и принадлежат отрезку [1; 4]. Проиллюстрируем решение на рисунке, построив график функции у = |t - 2| +|t - 3|.
Мы видим, что решения уравнения существуют при
но принадлежат отрезку [1; 4] лишь при а € [1; 3]. Ответ: а € [1; 3]. Задание 176. При каких а решения неравенства
образуют на числовой оси прямой отрезок длины 2|а|? Ответ:
Задание 177. При каких а решения неравенства
образуют на числовой оси прямой отрезок длины 3|а|? Решение: Данное неравенство равносильно совокупности систем:
при
а вторая — при
при
при
Объединяя решения систем, получаем: при
решением системы является отрезок
Его длина равна 3|а| в том случае, когда а (а < 0) удовлетворяет уравнению
то решения данного неравенства заполняют отрезок
Его длина равна
откуда
Ответ:
Задание 178. При каких а множество решений неравенства
содержит все целые отрицательные числа? Указание: Все целые отрицательные числа
являются решениями этого неравенства при выполнении условия
так как
Остается установить, при каких а числа х = -1 их = -2 также являются решениями этого неравенства. Ответ:
Решите следующие уравнения (179—182), сведя их к системе: Задание 179.
Ответ: При
при
при а
Задание 180.
Ответ:
при
Задание 181.
Решение: Очевидно, что
Если а = 0, то х = 0 — единственное решение уравнения. Рассматриваем далее значения а > 0. Полагая приходим к системе
Раскладывая последнее уравнение на множители и учитывая, что
имеем
Равенство
Оно справедливо при
При этом
Ответ: при
при
Задание 182.
Решение: Если а = 0, то решением уравнения является любое. число
Если же а # 0, то, умножая обе части равенства на
и сокращая на 2а, приходим к уравнению
Полагая
получаем систему
При этих а находим
Ответ: при
при
при
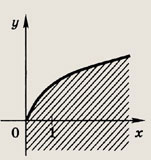
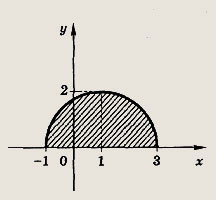
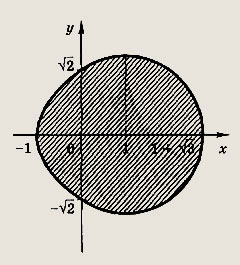
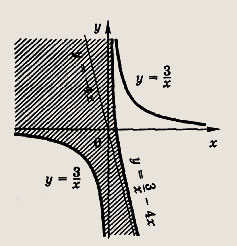
Ответ:
является часть параболы х - у2, расположенная в полуплоскости
На рис. штриховкой отмечено
также множество всех точек М(х; у), координаты которых удовлетворяют
Задание 183.
Ответ:
Задание 184.
Ответ:
Задание 185.
Ответ:
Задание 186.
Ответ:
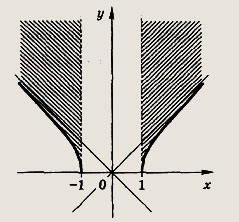
(часть гиперболы х2 - у2 = 1 в полуплоскости у > 0) Задание 187.
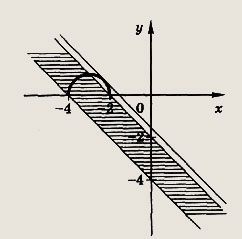
Решение: Нужно заштриховать область, координаты точек которой удовлетворяют системе неравенств
Прямые
касаются окружности
Задание 188.
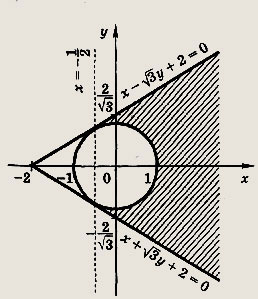
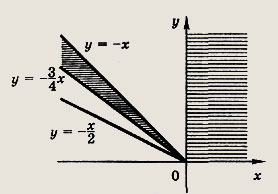
Решение: Нужно заштриховать множество точек, координаты которых удовлетворяют совокупности неравенств
При х < 0 она ограничена параболой
— окружностью (х - 1)2
+ у2 = 3. Задание 189.
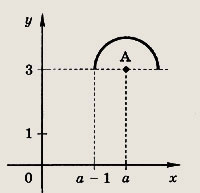
Что происходит с графиком функции при изменении параметра а? Указание: Это — верхняя половина окружности (х2 - а)2 + (у - З)2 = 1 с центром А(а; 3). При увеличении а полуокружность целиком смещается вправо. Ответ:
Задание 190.
Ответ:
Задание 191.
Ответ:
(область ограничена астроидой J\x\ + J\y] =1) Задание 192.
Указание: Возведя равенство в квадрат, приведите его к виду
Постройте этот график (гиперболу), складывая графики функций
Ответ:
Задание 193.
Решение: Неравенство равносильно совокупности систем
Решите следующие задачи (194—203), используя графики: Задание 194. Найдите значение параметра а, при которых уравнение
имеет ровно два решения. Ответ:
Задание 195. Найдите все а, при которых уравнение
Ответ:
Задание 196. Найдите все а, при которых уравнение имеет единственное решение. Решение: Запишем уравнение в виде
Первый график — это верхняя половина окружности у2 +(х + З)2 = 1. Графики прямых у = (1 - а) - х пересекают ось ординат в точках А (0; 1 - а). Мы видим, что уравнение имеет единственное решение при таких а, что
Кроме того, единственное решение получается и в том случае, если прямая у = (1 - а) - х — касательная к верхней половине окружности у2 + (х + З)2 = 1. Вычислив нужное значение а, получаем
Ответ:
Задание 197. Найдите все а, при которых уравнение
Указание: Постройте графики функций
Ответ:
Задание 198. При каких а уравнение
имеет единственное решение? Указание: Постройте графики функций
и проследите, что происходит с ними при изменении значения параметра а (см. задачу 189). Ответ: a € [2; 3) U (3; 4] Задание 199. При каких а система неравенств
Указание: Постройте область, координаты точек которой удовлетворяют неравенству
пересекается с указанной областью. Ответ:
Задание 200. Найдите все значения а, при которых система неравенств
Ответ:
Найдите все значения а, при каждом из которых система
Решение: Сделав замену переменных у + 3 = u; 5х = V, сведем задачу к следующей: найдем, при каких а система
(астроида; см задачу 191) и u2 + v2 = 16a (окружность радиуса
В силу их симметрии уравнение будет иметь четыре решения либо если окружность касается астроиды в этом случае, как легко видеть,
либо окружность проходит через точку А(1; 0)
Ответ:
Задание 202. Найдите все значения а, при которых всякая пара чисел (х; а), удовлетворяющая неравенству
Решение: Отметим штриховкой
в плоскости (х; а) области, где выполняются неравенства:
(вертикальная штриховка). Мы видим, что решения первого неравенства включают все решения второго неравенства лишь при а < а0. Для подсчета а0 найдем Х0 —- корень уравнения
Получаем х0 = -3, а тогда
Замечание. В отличие от всех предшествующих задач, где мы строили для обоснования графики стандартных функций (прямые, параболы, окружности и гиперболы), здесь мы опирались на построение графика функции
Поэтому приведенное решение можно признать недостаточно строгим (но полезным). Приведем другое решение этой задачи, просто решив неравенство
Сразу отметим, что при а > 0 решения этого неравенства не могут включать бесконечный интервал
Поэтому достаточно рассмотреть случай а < О. Неравенство
равносильно совокупности систем:
а вторая система — решение
Для выполнения условия задачи необходимо, чтобы
Ответ:
Задание 203. Найдите все отрицательные значения а, при которых числа х, не превосходящие по модулю числа
Ответ: а € [-1; 0)
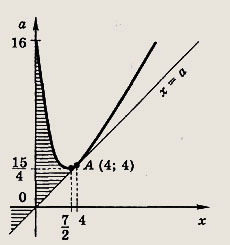
Решите системы неравенств (204—205): Задание 204.
Решение: Исходная система равносильна выполнению следующих условий:
Прямая х = а касается параболы а = х2 - 7х + 16 в точке А(4; 4). Решив уравнение х2 - 7х + 16 - а = 0, получим выражения
Ответ: при
при
при
Задание 205.
Ответ: При
при
при
при
Задание 206. При каких а неравенство
не имеет решений? Решение: Запишем неравенство в виде
и построим графики левой и правой частей этого неравенства. Рассмотрим два случая:
Если
то решений не будет при всех а > а0
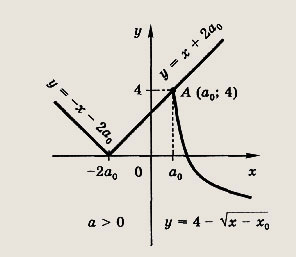
Число а0 находим из условия, что точка А(а0; 4) лежит на прямой у = х + 2а. Отсюда
Случай а < 0 несколько сложнее. Здесь нужное неравенство не будет иметь решений, если а < min(a1 a2), где число а1 находим из условия, что точка A(a1; 4) лежит на прямой у = -х - 2a1; а число a2 из условия, что
Получаем
Ответ:
Задание 207. При каких значениях параметра а система уравнений
Указание: См. задачу 186, где была построена подобная гипербола. Ответ:
Задание 208. При каких а система
Строим графики:
— верхнюю часть параболы;
Найдем среди этих прямых касательную к верхней части параболы и прямую, проходящую через точку (1; 0). Подсчеты дают для этих прямых значения
При всех
прямые пересекают эту часть параболы. Система имеет решения. Ответ:
Задание 209. Найдите наименьшее значение выражения
если х + 2у = 2. Ответ:
Задание 210. Найдите все пары чисел (х; у), удовлетворяющие уравнению х2 + у2 - 6x + 4у + 11 = 0, при которых значение выражения
наибольшее. Ответ:
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
|
|
|
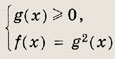
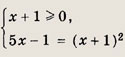
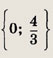
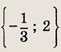
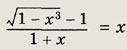
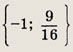
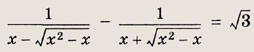
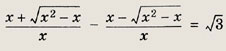
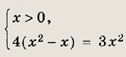
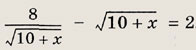
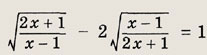
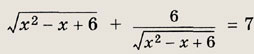
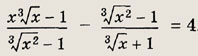
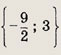
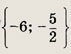
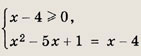
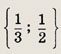
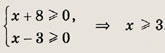
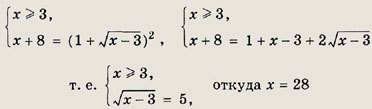
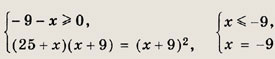
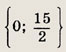
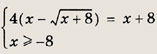
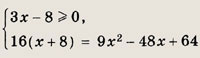
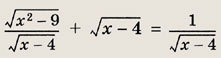
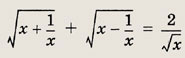
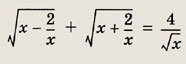
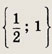
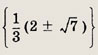
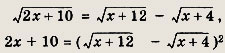
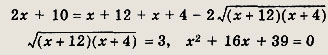
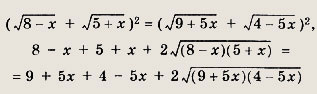
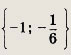
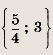

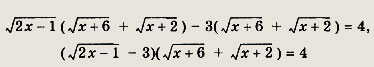
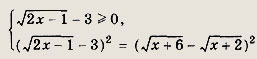
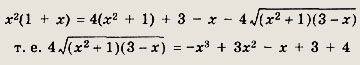
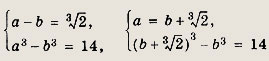
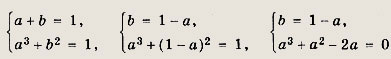
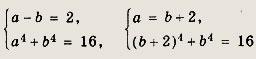
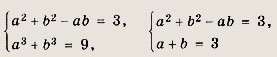
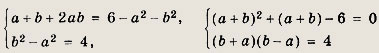
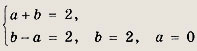
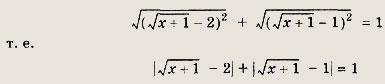
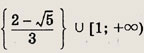
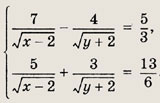
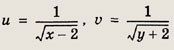

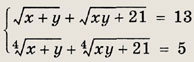
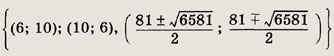
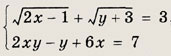
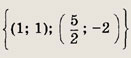
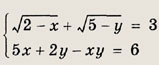
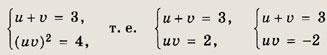
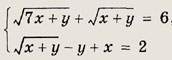
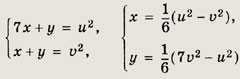
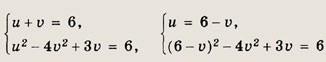

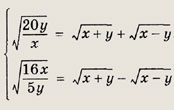
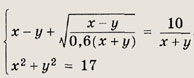
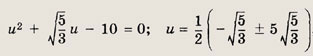

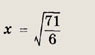
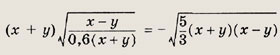
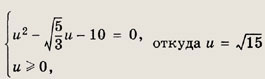

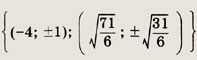
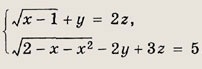
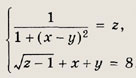
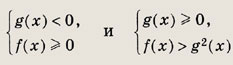
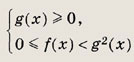
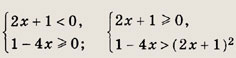
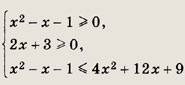
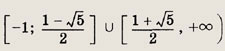
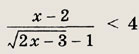
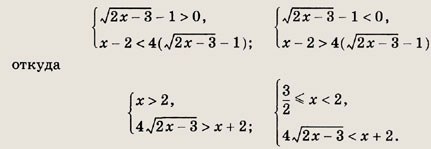
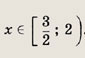
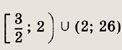
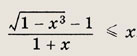
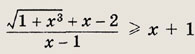
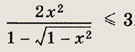
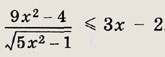
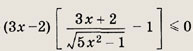
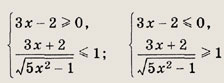
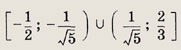
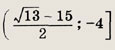

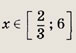
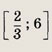
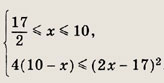
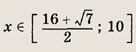
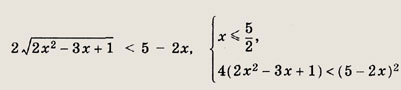
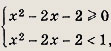
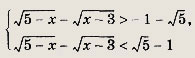
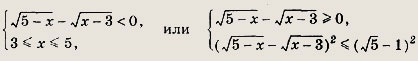
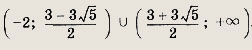
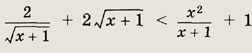
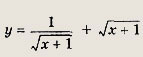
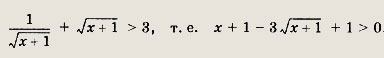
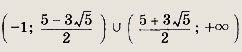
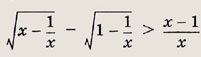
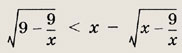
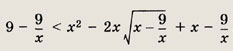
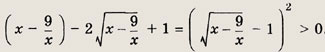
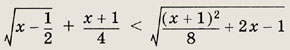
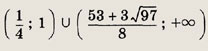
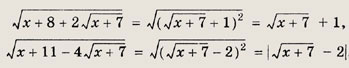
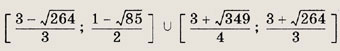

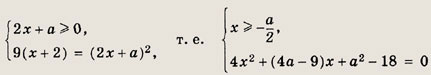
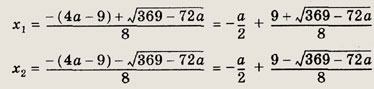
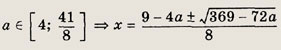
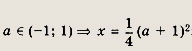
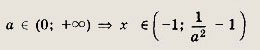
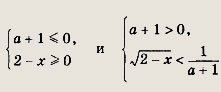
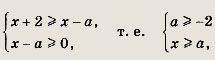
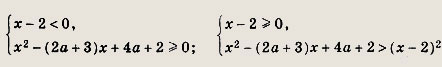

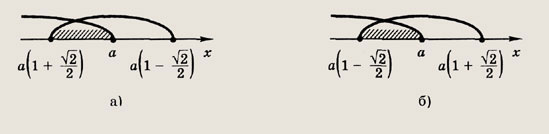
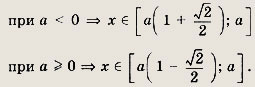
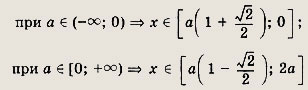
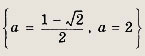
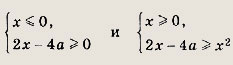
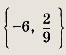

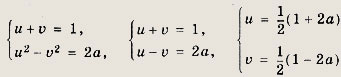
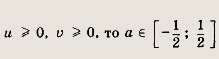
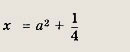

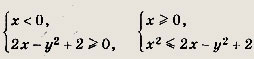
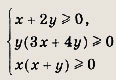
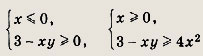
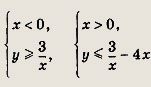
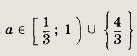
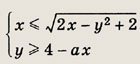
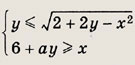
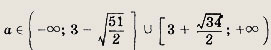
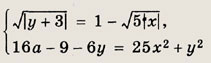
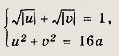
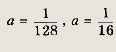
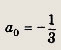
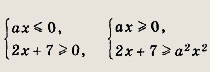
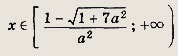

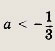
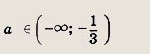
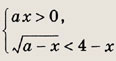
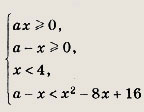
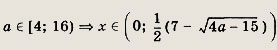
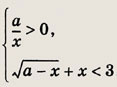
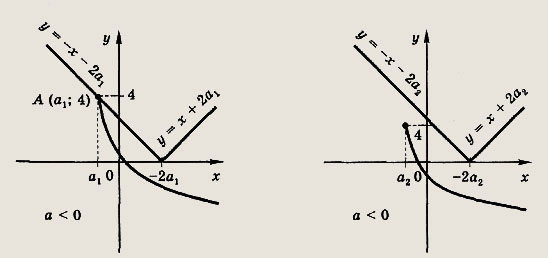
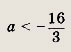
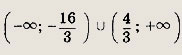
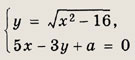
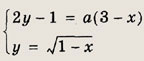
 Главная
Главная