Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Рис. 1 иллюстрирует эту ситуацию. Свободный протон (ион водорода) показан символически в центре в виде небольшого круга, помеченного знаком (+). Нейтральные атомы вокруг него показаны в форме несколько бо́льших кругов. Положение электронов в каждом атоме помеченного знаком (-), а положение связанных протонов знаком (+). Второй, третий и дальнейшие слои нейтральных атомов показаны только частично.

Так как кристалл является олицетворением определённого порядка, а он здесь (на рис. 1) явно имеется, то можно сказать, что вокруг свободного протона образуется своего рода кристалл из нейтральных атомов водорода.

Построение линейчатого спектра

Показанное на рис. 1 скопление атомов вокруг иона будет дальше для краткости называться сави. Проведём, исходя из иона в центре этого скопления, прямую OA. На этой прямой будут находиться атомы, представители каждого сферического слоя, расстояние которых от иона (протона) в центре ступенчато растёт. Пронумеруем атомы, находящиеся на этой прямой соответственно номеру слоя, начиная со внутреннего, цифрами 1, 2, 3 и т.д.. Соответствующими индексами n пометим расстояния rn от центра иона до соответствующего атома на этой прямой (n = 1, 2, 3 и т.д.).

Проделаем теперь мысленный эксперимент. Попробуем придать электрону атома 1 (рис. 1), который расположен наиболее близко к иону в центре сави, толчок в направлении иона. Если этот толчок будет достаточно сильным, то электрон сможет покинуть свой протон и образует с до этого свободным протоном новый нейтральный атом (водорода). Обозначим минимальную энергию, которая для этого понадобилась, знаком E1. Если бы мы сделали то же самое с электроном следующего атома на линии OA, с электроном атома 2, то требующаяся для отрыва электрона энергия была бы несколько больше, чем E1, так как атом 2 находится в области более слабого поля иона и его электрон притягивается ионом с меньшей силой, чем электрон атома 1. Обозначим эту энергию аналогично знаком E2 и отметим: E2 > E1. Повторив то же самое с электроном атома 3, мы из тех же соображений получим, что E3 > E2 и т.д.. Продолжая последовательно эти размышления, мы получим:

E1 < E2 < E3 < ... < En-1 < En < En+1 < ... < Ei              (1)

где En тем больше, чем больше n, но все En меньше, чем Ei. Ei здесь - значение энергии ионизации одиночного атома. Для случая водорода Ei = 13,53 eV. Разница между двумя соседними значениями энергии в этом неравенстве становится с ростом n всё меньше и меньше.

Представленные в ряду (1) значения энергий En являются энергиями поглощения. Эти порции энергии нужны электронам, чтобы переместиться к свободному протону. Так как спектр поглощения, как принято считать, идентичен спектру излучения, то можно предположить, что описанный выше ряд энергетических значений (1) аналогичен серии Лимана в спектре излучения водорода:

Em-1 = hcRy(1-1/m2) где m = 2,3,4...               (2)

Здесь h – постоянная Планка, c – скорость света, Ry – постоянная Ридберга.

Сравнение полученного спектра со спектром Лимана

Чтобы подтвердить это предположение соответствующим расчётом, необходимо было бы знать зависимость F(r) силы взаимодействия F между электроном и протоном в зависимости от расстояния r между ними, при расстояниях r меньше одного микрона. По принятой выше гипотезе эта зависимость должна выглядеть примерно так, как показано на рис. 2. Сила притяжения сперва растёт (примерно обратно пропорционально квадрату расстояния) по мере уменьшения расстояния, а затем быстро уменьшается до нуля и превращается в силу отталкивания, которая растёт ещё быстрей.

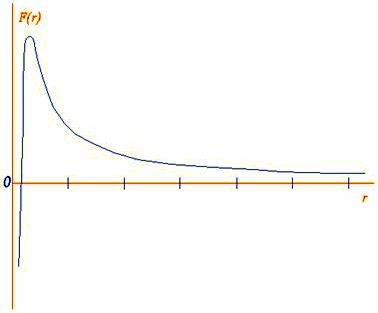
Рис. 2

Энергия, которую электрон получает в поле одиночного протона, можно выразить в соответствии с законом Кулона через интеграл C(1/ro - 1/r), или, что тоже самое, посредством выражения

C1(1 - r0/r) (3).

Нильс Бор в своё время сравнил выражение (3) с выражением (2) для частот серии Лимана, идентичное выражению C2 (1 - 1/n2), и понял, что отсюда можно получить

1/r ~ 1/n2 (4),

где значок (~) обозначает “пропорционально”. Если в последнем выражении текущее значение r заменить на дискретное rn, то из (4) немедленно следует: rn ~ n2. Полученный результат надо было после этого только истолковать. У любого человека r ассоциируется прежде всего с радиусом окружности. Орбита электрона в виде окружности уже была известна из толкования результата своих экспериментов Резерфордом (бывшего научного руководителя Нильса Бора). Бор сделал из произвольной окружности бесконечную серию “разрешённых”. Физического обоснования своего “поступка” он не дал. Это было чисто математическое толкование по принципу: “ведь совпадает с результатом”. Точно также “совпадали с результатом” расчёты астрономов по системе Птолемея – без понимания существа происходящего. (Кто-нибудь скажет: “А чем это плохо? Главное – умели рассчитать!” Разумеется, но, возможно, тогда не возникло бы понятия о силе тяжести. Не появились бы не только аппараты, которые тяжелее воздуха – самолёты и ракеты, но и те, что легче. Да, наверное, и многое другое – не появилось бы.)

Нильс Бор считал, что характерный спектр излучения (водорода) происходит от движений электрона в поле одиночного протона. Поэтому происхождение бесконечной серии частот излучения водорода можно было объяснить только за счёт идеи “сложного устройства” атома. В среде частично ионизированного газа (водорода) гораздо более естественно ожидать движение электрона от одного протона к другому. Это позволяет отказаться от идеи сложного устройства атома (атом водорода состоит только из двух элементарных, т.е. простых частиц!) Сложный спектр может получаться за счёт относительно сложного (по сравнению с атомом) устройства сави. Нейтральный атом из одного из слоёв сави “теряет” свой электрон, его принимает ион (свободный протон) в центре сави. Так как слои нейтральных атомов находятся на различном, ступенчато изменяющемся расстоянии от иона в центре сави, то ступенчато меняется и необходимая для ионизации обмена (отрыва электрона от своего протона в поле другого протона) энергия. Этими расстояниями определяется порционирование энергии поглощения. Чисто схематически электрон всегда движется между двумя протонами (рис. 3), от положения равновесия вблизи одного протона к положению равновесия вблизи другого. То есть математически мы будем иметь дело с наложением двух поворотно симметричных функций, силовым воздействием двух протонов на один электрон. Силовое поле, в котором при этом движется электрон, схематически показано на рис. 4. Вблизи своего протона в точке 1 электрон получает импульс (порцию энергии). В идеальном случае его хватает как раз на то, чтобы достигнуть точку ri посредине между двумя протонами, где силовое воздействие равно нулю. В этой точке, израсходовав всю энергию, скорость электрона тоже становится (практически) равной нулю. Дальше электрон движется в симметрично равном силовом поле к другому протону и, достигнув положения равновесия (точка 2), имеет ту же самую энергию и тот же самый импульс, который имел по выходе из точки 1. Так как электрон в точке 2 имеет некоторый импульс, т.е. скорость, то он в точке 2 не сможет остановиться и проскочит её. Начиная с точки 2 на электрон будет действовать отталкивающая сила, поэтому он будет вскоре остановлен и отброшен обратно. После того, как он снова минует положение равновесия, он будет снова притягиваться в сторону точки 2 и т.д. При этом колебательном движении электрон будет излучать энергию. После определённого числа колебаний, излучив всю полученную энергию, электрон займёт положение равновесия в точке 2. Таким образом, расстоянием между двумя протонами, обменивающимися электроном, порционируется не только энергия поглощения, но и излучения.

Рис. 3

Этим показана возможная физическая основа возникновения спектров поглощения и излучения. Кроме того, следует ещё показать, в соответствии с какими зависимостями должны изменяться кривые на рис. 2 и 4, чтобы получить соответствие полученной последовательности значений энергии (1) серии Лимана. Если в сави расстояние между слоями нейтральных атомов всегда одно и то же, тогда изменение функции S(n), представляющей последовательность площадей Si на рис. 4, будет пропорционально изменению интеграла от функции 1/r3, взятому в пределах от r0 до rn.

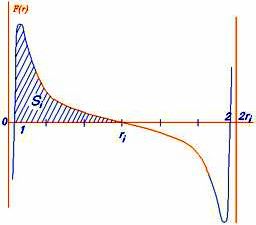
Рис. 4

Вместо выражения (3), применённого Бором, следует взять выражение для площади Si на рис. 4:

Sn = C3(1 - r02/rn2)           (5)

Рекомендуем скачать другие рефераты по теме: шпори скачать бесплатно, диплом школа.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата