Предыдущая страница реферата | 1  2  3

Любая модель проще реального объекта. Она отражает не все его свойства и характеристики, а только те, которые интересны нам в данном исследовании.

Перед тем, как использовать модель для изучения объекта необходимо доказать её подобие или адекватность реальному объекту. Существует много статистических методов такого доказательства.

Рассмотрим конкретные типы такого моделирования:

Физическое моделирование - это создание уменьшенных копий реальных объектов и систем. Примером физической модели в экологии является аквариум. Основным недостатком такого типа модели является то, что при обратно масштабном переходе, т.е. при увеличении размеров, некоторые закономерности, которые соблюдались на модели, соблюдаться перестают.

Концептуальное моделирование – это создание блок-схем, взаимодействие подсистемы процессов в пределах более сложных систем. Примером являются круговороты веществ.

Графическое моделирование – это изображение зависимости между переменными в одной из систем координат, чаще всего в прямоугольной декартовой системе. Примером являются графики изменений численности популяций.

Математическое моделирование – заключается в формализации поведения систем на основе математических выражений.

Существуют два принципиально разных подхода к математическому моделированию:

Формализация заведомо известных процессов, специфика и закономерности которых определены нами на основе наблюдений и экспериментов. Полученные закономерности изображаются в виде графических моделей, а затем, используя методы корреллеционного и регрессионного анализа, получают математические модели. Именно таким методом были получены формулы для расчёта предельно допустимого выброса. Математические модели, в данном случае, представляют собой системы алгебраических уравнений, чаще всего полиномов.

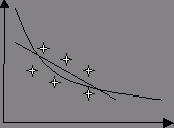
 Нужно получить зависимость у(х).

    У

                                                                       

                                                                                    х

           

Провели эксперимент, и для некоторых значений «х» получили экспериментальные точки.

Метод наименьших квадратов для получения модели. Согласно этому методу, кривая выбирается так, чтобы была минимальной, где - количество экспериментальных точек, - экспериментальное значение в точке , - значение модельной теоретической функции в точке .

Допустим, в качестве функции  мы выбрали линейную , тогда нам нужно определить значения параметров  и .

Чтобы функция имела минимум, необходимо, чтобы произведение по параметрам равнялось нулю.

          

               

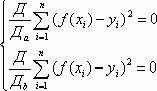
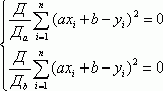
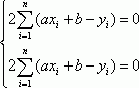
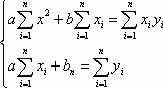
Второй подход заключается в выдвижении некоторой гипотезы о поведении системы и подбора математических выражений, описывающих некоторые физические законы, которые удовлетворяют этой гипотезе. Математические модели такого типа чаще всего представляют собой системы дифференциальных уравнений, полных или частных производных или системы интегральных уравнений, которые чаще всего решаются численно, но иногда аналитически, допустим с помощью преобразований Лапласа.

Скачали данный реферат: Тихомира, Челпанов, Shur'ev, Melitika, Церетели, Samarin.
Последние просмотренные рефераты на тему: контрольные 5 класс, гражданское право реферат, контрольная, реферат на тему.





Предыдущая страница реферата | 1  2  3