Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

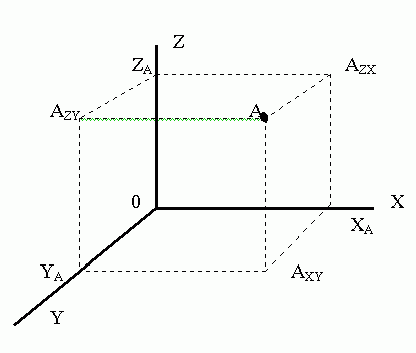
Рисунок 1. Точка А в пространстве и ее проекции на составляющие пространство плоскости

Плоскостями пространства соответственно являются - плоскости XY, XZ, YZ. Как легко увидеть из рисунка, точка А имеет три проекции на три ортогональные плоскости, а именно проекции AZX, AZY и AXY. Эти же проекции можно легко изобразить на эпюре. Для этого представим себе, что одна из осей пространства, например, Х разрезана пополам и вдоль. Тогда можно легко развернуть плоскости, составляющие пространство, и разложить их на одной плоскости (рисунок 2).

Отличительной особенностью эпюр является то, что на полученном рисунке дважды изображена "разрезанная пополам" ось Х. Как легко убедиться, на эпюрах изображены все три ортогональные плоскости пространства и на этих плоскостях легко поместились все три проекции точки А на каждую из плоскостей.

Читатель может убедиться сам в том, что, если имеется хотя бы две проекции любой точки в пространстве на две из ортогональных плоскостей, он может без труда на эпюрах найти координаты проекции этой точки на третью ортогональную плоскость. Именно поэтому часто говорят об эпюре как о чертеже, на котором пространственная фигура изображена методом двух ортогональных проекций на взаимно перпендикулярные, а затем развернутые плоскости.

Эпюры дают возможность более точного определения координат пространственной фигуры, изучения взаимного расположения точек фигуры в пространстве, выявления присущих им закономерностей.

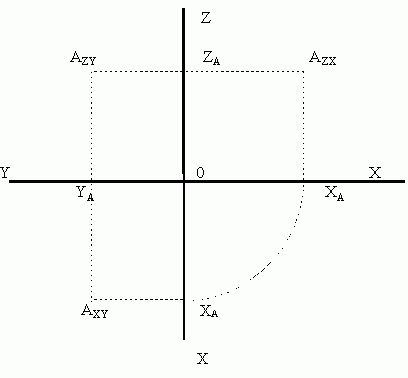
Рисунок 2. Эпюр точки, находящейся в пространстве X-Y-Z

В случае задачи, поставленной в данном параграфе, главным достоинством метода построения эпюра является то, что по двум имеющимся проекциям пространственной фигуры можно построить третью проекцию.

Очевидно, что если удалось построить эпюры одной точки в пространстве, то также легко можно построить эпюры двух, трех и более точек, расположенных в пространстве. Этим же способом можно построить и изучить проекцию не только любой, не связанной воедино совокупности точек, но и любой фигуры на каждую из плоскостей пространства, которая представляет собой некоторую связанную совокупность точек в пространстве. В этом уникальная особенность и важнейшее преимущество эпюров. Но, пожалуй, самое главное при этом - достигнуть абсолютной точности при построении третьей неизвестной проекции.

Это значит, что при наличии у исследователя проекции равновесной кривой товара А на плоскость "объем товара А - доход" и проекции равновесной кривой товара Б на плоскость "объем товара Б - доход", он может построить третью проекцию, а именно проекцию совместного распределения этих двух товаров (в зависимости от дохода потребителя) на плоскость "объем товара А - объем товара Б". Это изображение и является предметом исследования в теории потребительского поведения и принципиально может быть получена иным путем, чем в классической экономической теории.

В попытках трехмерного изображения ситуации на плоскости рисунка такой точности получить нельзя - возникают очень большие сложности с выверкой углов осей координат, пропорций и тому подобное.

В данной книге нет возможности более подробно останавливаться на методе построения эпюров. Для тех читателей, кому затруднительно использование методики построения эпюров, приведенных в этой книге, я рекомендую изучить любой учебник по начертательной геометрии, в котором обязательно есть раздел, посвященный вопросам построения эпюров.

Эпюр объемов распределения двух товаров повседневного спроса

Ранее мною было получено несколько типов равновесных кривых, попарное исследование которых с помощью эпюров может занять очень большой объем книги. Действительно, как следует из материалов параграфов 7 и 8 моей книги, существует четыре принципиально различных вида равновесных кривых (а сколько еще их возможных подвидов!). Совместное распределение этих кривых дает десять пар возможных распределений - кривая товара первого типа с аналогичной формы кривой другого товара (огурцы и помидоры, например), кривая товара первого типа с кривой товара второго типа и т.д. до пары - кривая товара четвертого типа с аналогичного рода товаром.

Для того, чтобы привести в некий порядок указанную возможную совокупность, рассмотрю вначале совместное распределение двух различных видов товара повседневного спроса.

При совместном рассмотрении указанных кривых для получения закономерности совместного распределения товаров возможно два принципиально различных случая.

Первый случай, о котором следует говорить, что он будет наиболее часто встречающимся в экономической практике, характеризуется тем, что проекции кривых каждого товара имеют отличный друг от друга вид. То есть они имеют разную размерность объемов; размах и месторасположение максимумов и минимумов, точек перегиба; отличные друг от друга асимптоты; углы наклонов и т.п.

Второй случай, возможный чисто теоретически, но вероятность его встречи на практике крайне мала - когда кривые имеют абсолютно одинаковый характер при одинаковом масштабе объемов. То есть эти кривые имеют одинаковую размерность объемов, размах и месторасположение максимумов и минимумов, точек перегиба, одинаковые асимптоты, углы наклонов и т.п.

Впрочем, это обстоятельство не является основанием для того, чтобы игнорировать полностью такую возможность и не рассматривать ее в моей теоретической работе.

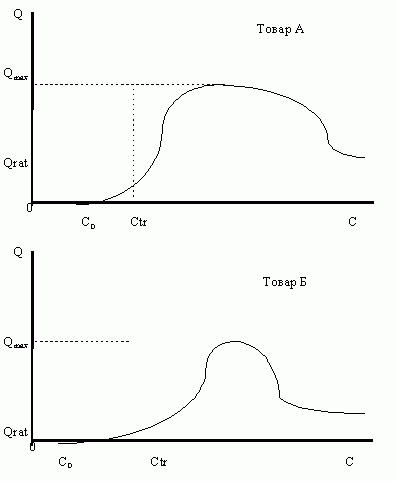
Рисунок 1. Проекции равновесных кривых товаров А и Б

На рисунке 1 изображены две проекции равновесных кривых на плоскости объем-доход, причем эти проекции отличны одна от другой. Для того, чтобы изобразить кривую совместного распределения объемов этих двух товаров в трехмерном пространстве в зависимости от дохода, необходимо представить, что это пространство определяют три ортогональные плоскости, а именно:

плоскость доход - объем товара А,

плоскость доход-объем товара Б,

Рекомендуем скачать другие рефераты по теме: контрольные работы 9 класс, налоги и налогообложение.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата