Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

б) K = 20000×(100×12/(100×12 – 10))12 = 20000×1.106 = 22132 д.е.

Задача 6. Номинальная годовая ставка – 30%. Найти уравнивающую процентную ставку при начислении сложных процентов каждые 3 месяца.

Решение

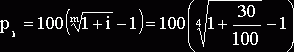= 6.779%.

Задача 7. По одному из вкладов в банке в течение 20 лет накоплено 200000д.е. Найти сумму, положенную на счет первоначально, если годовая процентная ставка (d) составляет 8%.

Решение

K0 = Kn×r-n = Kn×II8%20 = Kn×(1 + p/100)-n = 200000×(1 + 8/100)-20 =

= 200000×0.21454 = 42909 д.е.,

где r = (1 + p/100) – сложный декурсивный коэффициент.

Задача 8. Каждые три месяца в банк вкладывается по 500 д.е. Какова будет совокупная сумма этих вкладов в конце 10-го года при процентной ставке 8% и годовой капитализации.

Решение

Сначала для годовой процентной ставки 8% определим процентную уравнивающую ставку:

=1.9427%

Затем полученную уравнивающую ставку поместим в следующую формулу:

Svmn = u×, где rk = 1 + pk/100,

где         v – число вкладов в расчетном периоде,

               n - число лет,

               m – число капитализаций в год.

тогда

rk = 1 + 1.9427/100 = 1.0194

S4×10 = 500× = 500×60.8157 = 30407.84 д.е.

Задача 9. Насколько увеличатся годовые вклады по 2000д.е. в течение 4 лет при 8% годовых, если капитализация производится раз в три месяца и первый вклад вносится в конце первого года.

Решение

,

u1 = u×I2%4 / III2% = 2000×1.0824 / 4.204 = 514.93 д.е.

Рекомендуем скачать другие рефераты по теме: бесплатные банки рефератов, рефератов.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата