Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

3) кривые безразличия имеют отрицательный наклон каждой оси координат, при этом абсолютный наклон кривых уменьшается при движении в положительном направлении по каждой оси, т.е. кривые безразличия являются выпуклыми кривыми.

Перейдем к вопросу моделирования поведения потребителей в условиях товарно-денежных отношений на базе целевой функции потребления. В основе модели поведения потребителей лежит гипотеза, что потребители, осуществляя выбор товаров при установленных ценах и имеющемся доходе, стремятся максимизировать уровень удовлетворения своих потребностей. Пусть в пространстве п видов товаров исследуется поведение совокупности потребителей. Обозначим спрос потребителей через вектор У = (у1,у2..уn), а цены на различные товары.— через вектор Р = (р1,р2,—,Ра)- При величине дохода D потребители могут выбирать только такие комбинации товаров, которые удовлетворяют бюджетному ограничению ....

 Предположим, что предпочтение потребителей на множестве товаров выражается целевой функцией потребления U(Y). Тогда простейшая модель поведения потребителей : в векторной форме записи будет иметь вид:

U(Y) ®max;

PY£D

У>0.                 (1)

Геометрическая интерпретация модели (1) для двух агрегированных групп товаров представлена на рис.2.

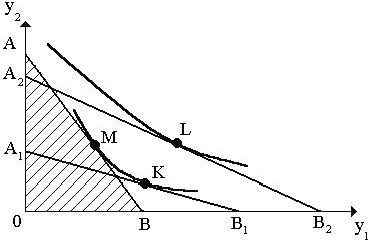
Рис.2.

Линия АВ (в других вариантах А1В1, А2В2) соответствует бюджетному ограничению и называется бюджетной линией Выбор потребителей ограничен треугольником АОВ  (А1ОВ1, А2ОВ2). Набор товаров М, соответствующий точке касания прямой АВ с наиболее отдаленной кривой безразличия, является оптимальным решением (в других вариантах это точки К и Л ).Легко заметить, что линии АВ и А1В1 соответствуют одному и тому же размеру дохода и разным ценам на товары у1 и у2.•Линия А2В2 соответствует большему размеру дохода.

Опираясь на некоторые выводы теории нелинейного программирования, можно определить математические условия оптимальности решений для модели (1). С задачей нелинейного программирования связывается так называемая функция Лагранжа, которая для задачи (1) имеет вид:

L(Y,l)=U(Y)+l(D-PY),

Где множитель Лагранжа l, является оптимальной оценкой дохода.

0бозначим частные производные функции U(Y)через Ui:

Ui=¶U(Y)/¶yi.

Эти производные интерпретируются как предельные полезные эффекты (предельные полезности) соответствующих потребительских благ и характеризуют прирост целевой функции потребления при увеличении использования 1-го блага (товара) на некоторую условную .«малую единицу».

Необходимыми условиями того, что вектор Y° будет оптимальным решением ,

являются условия Куна—Таккера:

Ui(Y°)£l°pi:    i=`1,`n,

При этом

Ui(Y°)=l°pi, если у° > 0 (товар приобретается),                       (2)

Ui(Y°)>l°pi,если yi°=0(товар не приобретается),PY°=D.          

Последнее из соотношений (2) соответствует полному использованию дохода,и для этого случая очевидно неравенство l°>0.•

Из условий оптимальности(2) следует, что

Ui(Y°)/pi=l°, yi°>0.

Это означает, что потребители должны выбирать товары таким образом, чтобы отношение предельной полезности к цене товара было одинаковым для всех приобретаемых товаров. Другими словами, в оптимальном наборе предельные полезности выбираемых товаров должны быть пропорциональны ценам.

Рекомендуем скачать другие рефераты по теме: решебники 10, контрольная работа 9.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата