Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

4) повышения средней часовой выработки 3155,2 - 2958,0 = +197,2 тыс. $.

Общее отклонение 3155,2 - 2803,8 = +351,4 тыс. $. Или 311,6 - 113,9 - 43,5 + 197,2 = +351,4.

При использовании МЦП очень важно обеспечить строгую пос­ледовательность подстановки: сначала выявляется влияние коли­чественных показателей, а потом - качественных. К качественным относятся, например, выработка, производительность труда, цена.

Факторный анализ с применением ЭВМ

Факторный анализ — это процедура установления силы влия­ния факторов на функцию или результативный признак (полез­ный эффект машины.элементы совокупных затрат, производитель­ности труда и т.д.) с целью ранжирования факторов для разработ­ки плана организационно-технических мероприятий по улучшению функции.

Применение методов факторного анализа требует большой под­готовительной работы и трудоемких по установлению моделей рас­четов. Поэтому без ЭВМ не рекомендуется применять методы кор­реляционного и регрессионного анализа, главных компонент. К тому же в настоящее время для ЭВМ различных классов имеются стандартные программы по этим методам. В свою очередь пользо­ваться установленными с помощью ЭВМ моделями очень просто.

На подготовительной стадии факторного анализа большое вни­мание следует уделять качеству матрицы исходных данных для ЭВМ. С этой целью сначала рекомендуется на основе логического анализа определять группы факторов, влияющих на исследуемую функцию.

К исходным данным предъявляются следующие требования:

а) в объем выборки должны включаться данные только по одно­родной совокупности объектов анализа, т.е. одного назначения и класса, используемых (изготавливаемых, функционирующих) в ана­логичных условиях по характеру и типу производства, режиму работы, географическому району и т.д. В том случае, когда необ­ходимо увеличить размер матрицы, исходные данные отдельных объектов могут быть приведены в сравнимый вид с большинством объектов по отличающимся признакам путем умножения их на корректирующие, коэффициенты;

б) период динамического ряда исходных данных должен быть небольшим, но, по возможности, одинаковым для всех объектов. Устойчивый период упреждения (зона прогноза) обычно в два и более раза меньше периода динамического ряда. Например, по дан­ным за 1985-1995гг. можно разработать прогноз до 2000г., а в пос­ледующие годы по фактическим данным модель должна обновляться (уточняться);

в) исходные данные должны быть качественно однородными, с небольшими интервалами между собой;

г) следует применять одинаковые методы или источники фор­мирования данных. Если динамический ряд имеет крупные струк­турные сдвиги (например из-за изменения цен, ассортимента вы­пускаемой продукции, программы ее выпуска и т.д.), то все дан­ные должны быть приведены в сравнимый вид или одинаковые условия;

д) отдельные исходные данные должны быть независимы от предыдущих и последующих наблюдений.

Например, наблюдение не должно определяться расчетным путем по предыдущему на­блюдению.

Основные параметры корреляционно-регрессионного анализа в связи с их сложностью не приводятся, поскольку все расчеты предполагается выполнять на ЭВМ по стандартной программе. Ко­нечные результаты расчета выдаются на печать (табл. 4.3).

Факторный анализ следует проводить в следующей последова­тельности:

1. Обоснование объекта анализа, постановка цели.

2. Сбор исходных данных и их уточнение в соответствии с ранее описанными требованиями.

            Основные параметры корреляционно- регрессионного анализа.

Назначение параметра	Обозначение	Что характеризует параметр и для чего применяется	Оптимальное значение параметра
1. Объем выработки		Количество данных по фактору (размер матрицы по вертикали). Применяется для установления тенденций изменения фактора	Не менее чем в 3-5 раз больше количества факторов (Nxi)
2. Коэффициент вариации	Vi	Уровень отклонения значений факторов от средней анализируемой совокупности	Меньше 33%
3. Коэффициент парной корреляции	Rxy	Тесноту связи между i-м фактором и функцией. Применяется для отбора факторов	Больше  0,1
4. Коэффициент частной корреляции	Rxx	Тесноту связи между факторами. Применяется для отбора факторов	Чем меньше, тем лучше модель
5. Коэффициент множественной корреляции		Тесноту связи одновременно между всеми факторами и функцией. Применяется для выбора модели	Больше 0,7
6. Коэффициент множественной детерминации		Долю влияния на функцию включенных в модель факторов. Равен квадрату коэффициента множественной корреляции	Больше 0,5
7. Коэффициент  асиметрии		Степень отклонения фактического распределения случайных наблюдений от нормального по центру распределения. Применяется для проверки нормальности распределения	Метод наименьших квадратов может применяться при А меньше трёх
8. Коэффициент эксцесса		Плосковершинность случайных наблюдений от нормального  по центру распределения. Применяется для проверки нормальности распределения функции	Е должен быть меньше трёх
9. Критерий Фишера		Математический критерий характеризующий значимость уравнения регрессии. Применяется для выбора модели	F должен быть больше табличного значения, установленного для различных размеров матрицы и вероятностей
10. Критерий Стьюдента		Существенность факторов, входящих в модель. Применяется для выбора модели	Больше 2 (при вероятности, равной 0,95
11. Среднеквадратическая ошибка коэффициентов регрессии	ai	Точность полученных коэффициентов регрессии. Применяется для оценки коэффициентов регрессии	В 2 и более раза меньше соответствующего коэффициента регрессии
12. Ошибка аппроксимации		Допуск прогноза или степень несоответствия эмпирической зависимости теоретической. Применяется для оценки адекватности (точности) модели	Меньше +-15%
13. Коэффициент эластичности	Эi	Показывает, на сколько процентов изменяется функция при изменении соответствующего фактора на 1%. Применяется для ранжирования факторов по их значимости	Больше 0,01

3. Построение гистограмм по каждому фактору с целью определения форм распределения случайных наблюдений.

            Построение по каждому фактору корреляционных полей, т.е. графическое изображение функций от фактора с целью предварительного определения тесноты и формы связи между функцией и каждым фактором. Примеры корреляционных полей показаны на рис 4.2.

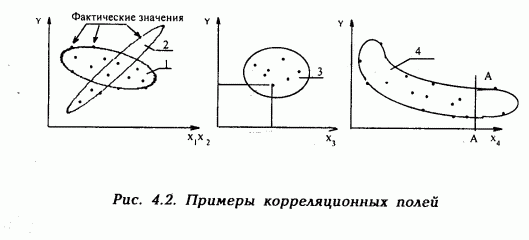Корреляционные поля построены по исходным статистичес­ким данным X)—Х4 (факторы) и Y (функция). Анализ корреляци­онных полей показывает, что:

а) между Y и X1 теснота связи слабая, по форме она линейная, обратно пропорциональная;

б) между Y и Х2 теснота связи высокая, по форме она линейная, прямо пропорциональная;

в) между Y и Х3 связи нет, т.к. функцию Y = f(X3) можно про­вести в любом направлении;

Рекомендуем скачать другие рефераты по теме: шпаргалки по математике, bestreferat.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата