
–Р–љ–∞–ї–Є–Ј —Д—Г–љ–Ї—Ж–Є–Є —Д–Є–ї—М—В—А–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –і–ї—П –љ–µ—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П –њ—А–Є—В–Њ–Ї–∞ –ґ–Є–і–Ї–Њ—Б—В–Є (–≥–∞–Ј–∞) –Ї –љ–µ—Б–Њ–≤–µ—А—И–µ–љ–љ–Њ–є —Б–Ї–≤–∞–ґ–Є–љ–µ
| –Ъ–∞—В–µ–≥–Њ—А–Є—П —А–µ—Д–µ—А–∞—В–∞: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –≥–µ–Њ–≥—А–∞—Д–Є–Є
| –Ґ–µ–≥–Є —А–µ—Д–µ—А–∞—В–∞: –≤–∞—А–Є–∞–љ—В—Л –Њ—В–≤–µ—В–Њ–≤, —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
| –Ф–Њ–±–∞–≤–Є–ї(–∞) –љ–∞ —Б–∞–є—В: Selidov.
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3
–≥–і–µ ki вАФ —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А—П–Љ–Њ–є, –Ї–Њ—В–Њ—А—Л–є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П h –Є –Њ—В –Є–љ–і–µ–Ї—Б–∞ j –љ–µ –Ј–∞–≤–Є—Б–Є—В.
–Р–љ–∞–ї–Є–Ј –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –њ–Њ–≤–µ–і–µ–љ–Є—П –і–µ¬≠–њ—А–µ—Б—Б–Є–Є Dp*i,j –Њ—В f0 –і–ї—П –≤—Б–µ—Е rc >0,01 –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –≥—А–∞—Д–Є–Ї–Є —Н—В–Њ–є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –њ—Г—З–Ї–∞ –њ—А—П–Љ—Л—Е –і–ї—П –ї—О–±–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П h. –Ф–ї—П rc< 0,01 –≤ –≥—А–∞—Д–Є–Ї–∞—Е –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –њ–Њ—П–≤–ї—П—О—В—Б—П –љ–∞—З–∞–ї—М–љ—Л–µ –љ–µ–ї–Є–љ–µ–є–љ—Л–µ —Г—З–∞¬≠—Б—В–Ї–Є, –њ–µ—А–µ—Е–Њ–і—П—Й–Є–µ –њ—А–Є¬†¬† –і–∞–ї—М–љ–µ–є—И–µ–Љ —Г–Љ–µ–љ—М—И–µ–љ–Є–Є –њ–∞—А–∞–Љ–µ—В—А–∞ f0 (–Є–ї–Є –ґ–µ –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є –µ–≥–Њ –Њ–±—А–∞—В–љ–Њ–є¬† –≤–µ–ї–Є—З–Є–љ—Л 1/foj) –≤ –њ—А—П–Љ—Л–µ –і–ї—П –≤—Б–µ—Е –Ј–љ–∞—З–µ–љ–Є–є h<l,0
(—А–Є—Б. 2). –Я—А–Є h=l,0 –њ–Њ–≤–µ–і–µ–љ–Є–µ –і–µ–њ—А–µ—Б¬≠—Б–Є–Є —Б—В—А–Њ–≥–Њ –ї–Є–љ–µ–є–љ–Њ. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –њ—А–Њ—В—П¬≠–ґ–µ–љ–љ–Њ—Б—В—М –љ–µ–ї–Є–љ–µ–є–љ–Њ–≥–Њ —Г—З–∞—Б—В–Ї–∞ –і–ї—П —А–∞–Ј¬≠–љ—Л—Е rc –њ—А–Є h=const —А–∞–Ј–ї–Є—З–љ–∞. –Ш —З–µ–Љ –Љ–µ–љ—М—И–µ –Ј–љ–∞—З–µ–љ–Є–µ –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–Њ–≥–Њ —А–∞–і–Є¬≠—Г—Б–∞ rc , —В–µ–Љ –±–Њ–ї—М—И–µ –њ—А–Њ—В—П–ґ–µ–љ–љ–Њ—Б—В—М –љ–µ¬≠–ї–Є–љ–µ–є–љ–Њ–≥–Њ —Г—З–∞—Б—В–Ї–∞ (—А–Є—Б. 2).
2. –Ю–њ—А–µ–і–µ–ї–Є–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ R(rc, h, f0) –Є –µ–µ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Л—Е –њ–∞¬≠—А–∞–Љ–µ—В—А–Њ–≤ rc, h, f0.
–Ч–љ–∞—З–µ–љ–Є—П R(rc, h, f0) —А–∞—Б—Б—З–Є—В–∞–љ—Л –і–ї—П —В–µ—Е –ґ–µ –≤–µ–ї–Є—З–Є–љ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ rc, h, f0. –Ї–Њ¬≠—В–Њ—А—Л–µ —Г–Ї–∞–Ј–∞–љ—Л –≤ –њ—Г–љ–Ї—В–µ 1, –Њ–±—А–∞–±–Њ—В–Ї–∞ —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ —В–∞–Ї–ґ–µ –∞–љ–∞–ї–Њ–≥–Є—З–љ–∞. –Я–µ—А–µ—Е–Њ–і –Њ—В –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ¬≠–љ–Є—П R(rc, h, f0) –Ї –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є R*i,j (rc) –Њ—Б—Г—Й–µ—Б—В–≤–ї–µ–љ —Б–Њ–≥–ї–∞—Б–љ–Њ –≤—Л—А–∞–ґ–µ–љ–Є—О
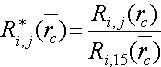 .¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬†¬† (13)
.                                                                             (13)
–Р–љ–∞–ї–Є–Ј –њ–Њ–≤–µ–і–µ–љ–Є—П R*i,j (rc) –Є —А–µ–Ј—Г–ї—М¬≠—В–∞—В—Л –Њ–±—А–∞–±–Њ—В–Ї–Є —А–∞—Б—З–µ—В–љ–Њ–≥–Њ –Љ–∞—В–µ—А–Є–∞–ї–∞, –≥–і–µ —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–∞ –µ–µ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В –њ–∞¬≠—А–∞–Љ–µ—В—А–Њ–≤ rc, h, f0, —З–∞—Б—В–Є—З–љ–Њ –њ—А–Є–≤–µ–і–µ–љ—Л –љ–∞ —А–Є—Б, 2 (–Ї—А–Є–≤—Л–µ –і–∞–љ—Л –њ—Г–љ–Ї—В–Є—А–Њ–Љ).
–Я—А–Є –≥c >0,01 –і–ї—П –ї—О–±–Њ–≥–Њ hi R*i,j (rc) —Г–ґ–µ –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В f0i .
–Ш–Ј –∞–љ–∞–ї–Є–Ј–∞ –і–∞–љ–љ—Л—Е —А–∞—Б—З–µ—В–∞ –Є –≥—А–∞—Д–Є¬≠–Ї–Њ–≤ —А–Є—Б. 2 —Б–ї–µ–і—Г–µ—В: –њ—А–Є rc<0,01 –≤ –њ–Њ¬≠–≤–µ–і–µ–љ–Є–Є R*i,j (rc) –і–ї—П –≤—Б–µ—Е h<l,0 –љ–∞¬≠–±–ї—О–і–∞–µ—В—Б—П –љ–µ–ї–Є–љ–µ–є–љ—Л–є —Г—З–∞—Б—В–Њ–Ї, –њ–µ—А–µ—Е–Њ¬≠–і—П—Й–Є–є —Б –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П f0 (—В–Њ—З–Ї–∞ –° –љ–∞ –≥—А–∞—Д–Є–Ї–µ) –≤ –њ—А—П–Љ—Г—О –ї–Є–љ–Є—О, –њ–∞—А–∞–ї¬≠–ї–µ–ї—М–љ—Г—О –Њ—Б–Є –∞–±—Б—Ж–Є—Б—Б. –Т–∞–ґ–љ–Њ –Њ—В–Љ–µ—В–Є—В—М,
—З—В–Њ –і–ї—П –Њ–і–љ–Њ–≥–Њ –Є —В–Њ–≥–Њ –ґ–µ –Ј–љ–∞—З–µ–љ–Є—П rc –∞–±—Б—Ж–Є—Б—Б–∞ —В–Њ—З–Ї–Є –њ–µ—А–µ—Е–Њ–і–∞ –љ–µ–ї–Є–љ–µ–є–љ–Њ–≥–Њ —Г—З–∞—Б—В–Ї–∞ –≤ –ї–Є–љ–µ–є–љ—Л–є –і–ї—П R*i,j (rc) –Є–Љ–µ–µ—В —В–Њ –ґ–µ —Б–∞–Љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —З—В–Њ –Є –∞–±—Б—Ж–Є—Б—Б–∞ —В–Њ—З–µ–Ї –њ–µ—А–µ—Е–Њ–і–∞ –і–ї—П –≥—А–∞—Д–Є–Ї–Њ–≤ –Ј–∞–≤–Є—Б–Є¬≠–Љ–Њ—Б—В–Є Dp*i,j (rc) –Њ—В ln(l/f0i ) (–ї–Є–љ–Є—П CD). –Э–∞—З–Є–љ–∞—П —Б —Н—В–Њ–≥–Њ –Љ–Њ–Љ–µ–љ—В–∞, R*i,j (rc) –і–ї—П –і–∞–љ–љ–Њ–≥–Њ rc –њ—А–Є –і–∞–ї—М–љ–µ–є—И–µ–Љ –љ–∞–±–ї—О–і–µ–љ–Є–Є –Ј–∞–≤–Є—Б–Є—В –љ–µ –Њ—В –≤—А–µ–Љ–µ–љ–Є, –∞ —В–Њ–ї—М–Ї–Њ –Њ—В hi вАҐ –Ш —З–µ–Љ –≤—Л—И–µ —Б—В–µ–њ–µ–љ—М –≤—Б–Ї—А—Л—В–Є—П, —В. –µ. —З–µ–Љ —Б–Њ–≤–µ—А—И–µ–љ–љ–µ–µ —Б–Ї–≤–∞–ґ–Є–љ–∞,. —В–µ–Љ –Љ–µ–љ—М—И–µ –±—Г¬≠–і–µ—В –Ј–љ–∞—З–µ–љ–Є–µ R*i,j (rc) –Ш –њ—А–Є h=l (—Б–Ї–≤–∞¬≠–ґ–Є–љ–∞ —Б–Њ–≤–µ—А—И–µ–љ–љ–∞—П –њ–Њ —Б—В–µ–њ–µ–љ–Є –≤—Б–Ї—А—Л¬≠—В–Є—П) —Д—Г–љ–Ї—Ж–Є—П —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П —А–∞–≤–љ–∞ –љ—Г¬≠–ї—О. –Ю—З–µ–≤–Є–і–љ–Њ, –љ–µ–ї–Є–љ–µ–є–љ–Њ—Б—В—М Dp*i,j (rc) —Б–≤—П–Ј–∞–љ–∞ —Б —Е–∞—А–∞–Ї—В–µ—А–Њ–Љ –њ–Њ–≤–µ–і–µ–љ–Є—П —Д—Г–љ–Ї¬≠—Ж–Є–Є —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П, –Ї–Њ—В–Њ—А–∞—П, –≤ —Б–≤–Њ—О –Њ—З–µ¬≠—А–µ–і—М, –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–∞ –§—Г—А—М–µ. –Ю—В¬≠–Љ–µ—В–Є–Љ —В–∞–Ї–ґ–µ, —З—В–Њ –≤ —В–Њ—З–Ї–µ –° (—А–Є—Б. 2) —З–Є—Б–ї–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —Б–Њ–њ—А–Њ—В–Є–≤¬≠–ї–µ–љ–Є—П —Б—В–∞–љ–Њ–≤–Є—В—Б—П —А–∞–≤–љ—Л–Љ –Ј–љ–∞—З–µ–љ–Є—О —Д–Є–ї—М—В—А–∞—Ж–Є–Њ–љ–љ—Л—Е —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є–є (C1(rc, h)) –і–ї—П –њ—А–Є—В–Њ–Ї–∞¬† —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П —А–µ¬≠–ґ–Є–Љ–∞.
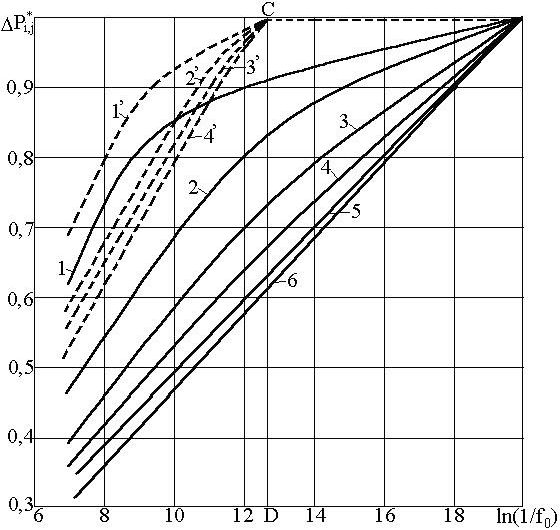
–†–Є—Б. 2. –Я–Њ–≤–µ–і–µ–љ–Є–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є –і–µ–њ—А–µ—Б¬≠—Б–Є–Є –Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —Д–Є–ї—М—В—А–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П¬†¬† (rc=0,0014,¬† h=const, f0) –њ—А–Є h, —А–∞–≤–љ—Л—Е: 1,1'вАФ0,1; 2,2'вАФ 0,3; 3,3'вАФ0,5;¬† 4,4'вАФ0,7;¬†¬† 5,5'вАФ 0,9; 6,6'вАФ 1,0.
–≤—Л–≤–Њ–і—Л
1. –Ф–µ–њ—А–µ—Б—Б–Є—П –љ–∞ –Ј–∞–±–Њ–µ –љ–µ—Б–Њ–≤–µ—А—И–µ–љ–љ–Њ–є –њ–Њ —Б—В–µ–њ–µ–љ–Є –≤—Б–Ї—А—Л—В–Є—П —Б–Ї–≤–∞–ґ–Є–љ—Л –і–ї—П –≤—Б–µ—Е rc < 0,01 –Є–Љ–µ–µ—В –і–≤–∞ —П–≤–љ–Њ –≤—Л—А–∞–ґ–µ–љ¬≠–љ—Л—Е –Ј–∞–Ї–Њ–љ–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є—П: –∞) –љ–µ–ї–Є–љ–µ–є–љ—Л–є, –Ї–Њ—В–Њ—А—Л–є –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О —Д—Г–љ–Ї¬≠—Ж–Є–Є —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П –Њ—В –≤—А–µ–Љ–µ–љ–Є –Є —Б–Њ–Њ—В¬≠–≤–µ—В—Б—В–≤—Г–µ—В –љ–µ—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Г—Б—П –њ—А–Є—В–Њ–Ї—Г —Б–ґ–Є–Љ–∞–µ–Љ–Њ–є –ґ–Є–і–Ї–Њ—Б—В–Є (–≥–∞–Ј–∞); –±) –ї–Є–љ–µ–є¬≠–љ—Л–є, –Ї–Њ—В–Њ—А—Л–є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Ї–≤–∞–Ј–Є—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Г—Б—П –њ—А–Є—В–Њ–Ї—Г –Є –љ–µ —Б–≤—П–Ј–∞–љ —Б —Д—Г–љ–Ї—Ж–Є–µ–є —Б–Њ–њ—А–Њ—В–Є–≤–ї–µ–љ–Є—П.
2. –Т–µ–ї–Є—З–Є–љ–∞ R(rc, h, f0) –і–ї—П –љ–µ—Г—Б—В–∞¬≠–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П –њ—А–Є—В–Њ–Ї–∞ –Ї–∞—З–µ—Б—В–≤–µ–љ–љ–Њ –Њ–њ–Є¬≠—Б—Л–≤–∞–µ—В –°1(rc, h) –і–ї—П —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П, –Є –µ–µ —З–Є—Б–ї–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ—А–Є –ї—О–±–Њ–Љ –≤—Б–Ї—А—Л¬≠—В–Є–Є –њ–ї–∞—Б—В–∞ –≤—Б–µ–≥–і–∞ –Љ–µ–љ—М—И–µ —З–Є—Б–ї–µ–љ–љ–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П –°1(rc, h) –њ—А–Є —Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Б—П –њ—А–Є—В–Њ–Ї–µ.
3. –Я–Њ–ї—Г—З–µ–љ–љ–Њ–µ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Њ–µ —А–µ—И–µ¬≠–љ–Є–µ –і–ї—П –љ–µ—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П –њ—А–Є—В–Њ–Ї–∞ —Б–ґ–Є–Љ–∞–µ–Љ–Њ–є –ґ–Є–і–Ї–Њ—Б—В–Є (–≥–∞–Ј–∞) –Ї –љ–µ—Б–Њ–≤–µ—А¬≠—И–µ–љ–љ–Њ–є —Б–Ї–≤–∞–ґ–Є–љ–µ –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–Љ –њ–Њ –њ—А–Њ¬≠—В—П–ґ–µ–љ–љ–Њ—Б—В–Є¬† –њ–ї–∞—Б—В–µ¬† –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Њ –≤ –њ—А—П–Љ–Њ–ї–Є–љ–µ–є–љ—Г—О –∞–љ–∞–Љ–Њ—А—Д–Њ–Ј—Г, –Ї–Њ—В–Њ—А–∞—П –њ–Њ–Ј–≤–Њ–ї—П–µ—В —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –Є–љ—В–µ—А–њ—А–µ—В–Є—А–Њ–≤–∞—В—М –Ї—А–Є–≤—Л–µ –≤–Њ—Б—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є—П –Ј–∞–±–Њ–є–љ–Њ–≥–Њ –і–∞–≤¬≠–ї–µ–љ–Є—П.
4. –Т—Л–±–Њ—А¬† fo, –і–∞—О—Й–µ–≥–Њ¬†¬† –Ј–љ–∞—З–µ–љ–Є—П Dp*i,j(rc)=1, –љ–µ –≤–ї–Є—П–µ—В –љ–∞ –њ—А–Њ—В—П–ґ–µ–љ¬≠–љ–Њ—Б—В—М –љ–µ–ї–Є–љ–µ–є–љ–Њ–≥–Њ —Г—З–∞—Б—В–Ї–∞, —Б–Њ–Њ—В–≤–µ—В—Б—В¬≠–≤—Г—О—Й–µ–≥–Њ –љ–µ—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–Љ—Г—Б—П –і–≤–Є–ґ–µ–љ–Є—О, –љ–∞ –≥—А–∞—Д–Є–Ї–Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є Dp*i,j(rc) –Њ—В ln(1/f0i).
–Ы–Ш–Ґ–Х–†–Р–Ґ–£–†–Р
1. –Ґ –µ –ї –Ї –Њ –≤ –Т. –Р. –Я—А–Є—В–Њ–Ї –Ї —В–Њ—З–µ—З–љ–Њ–Љ—Г —Б—В–Њ–Ї—Г –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Є –Ї –ї–Є–љ–Є–Є —Б—В–Њ–Ї–Њ–≤ –≤ –њ–Њ–ї—Г –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–Љ –њ–ї–∞—Б—В–µ. –Э–Ґ–°. –Т—Л–њ. 30, –£—Д–∞, 1975.
2. –Ы –µ –Њ –љ –Њ –≤ –Т. –ШвАЮ –Ґ–µ–ї–Ї–Њ–≤ –Т. –Р., –Ъ–∞–њ—В–µ–ї–Є–љ–Є–љ –Э. –Ф. –°–≤–µ–і–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –љ–µ—Г—Б—В–∞–љ–Њ–≤–Є–≤—И–µ–≥–Њ—Б—П –њ—А–Є—В–Њ–Ї–∞¬†¬† —Б–ґ–Є–Љ–∞–µ–Љ–Њ–є –ґ–Є–і–Ї–Њ—Б—В–Є (–≥–∞–Ј–∞) –Ї –љ–µ—Б–Њ–≤–µ—А—И–µ–љ–љ–Њ–є —Б–Ї–≤–∞–ґ–Є¬≠–љ–µ –Ї —А–µ—И–µ–љ–Є—О —Г—А–∞–≤–љ–µ–љ–Є—П –њ—М–µ–Ј–Њ–њ—А–Њ–≤–Њ–і–љ–Њ—Б—В–Є. –Ґ–µ–Ј–Є—Б—Л –і–Њ–Ї–ї–∞–і–Њ–≤ –љ–∞ XIII –љ–∞—Г—З–љ–Њ-—В–µ—Е–љ–Є—З–µ¬≠—Б–Ї–Њ–Љ —Б–µ–Љ–Є–љ–∞—А–µ –њ–Њ –≥–Є–і—А–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–Љ –Љ–µ¬≠—В–Њ–і–∞–Љ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є –Є –Ї–Њ–љ—В—А–Њ–ї—О –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ —А–∞–Ј—А–∞–±–Њ—В–Ї–Є –љ–µ—Д—В—П–љ—Л—Е –Љ–µ—Б—В–Њ—А–Њ–ґ–і–µ–љ–Є–є. –Я–Њ–ї¬≠—В–∞–≤–∞, 1976.
3. –С –∞ —Е –≤ –∞ –ї –Њ –≤ –Э. –°. –І–Є—Б–ї–µ–љ–љ—Л–µ –Љ–µ—В–Њ¬≠–і—Л. –Ш–Ј–і-–≤–Њ ¬Ђ–Э–∞—Г–Ї–∞¬ї, –Ь., 1974.
–°–Ї–∞—З–∞–ї–Є –і–∞–љ–љ—Л–є —А–µ—Д–µ—А–∞—В: Kozin, –С—Г–і–љ–Є–Ї–Њ–≤, Dominik, Jusupov, Werbina, –Э–µ–≥–Є–љ, Azar.
–Я–Њ—Б–ї–µ–і–љ–Є–µ –њ—А–Њ—Б–Љ–Њ—В—А–µ–љ–љ—Л–µ —А–µ—Д–µ—А–∞—В—Л –љ–∞ —В–µ–Љ—Г: —А–µ—Д–µ—А–∞—В –њ–Њ –Ї—Г–ї—М—В—Г—А–Њ–ї–Њ–≥–Є–Є, –∞–ї–µ–Ї—Б–∞–љ–і—А —А–µ—Д–µ—А–∞—В, –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л–µ —А–µ—Д–µ—А–∞—В—Л, –±–∞–љ–Ї —А–µ—Д–µ—А–∞—В–Њ–≤.
–Ъ–∞—В–µ–≥–Њ—А–Є–Є:
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3
 –У–ї–∞–≤–љ–∞—П
–У–ї–∞–≤–љ–∞—П