Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Высота приведенного уровня в зоне Марианской впадины равна -8424 м (полагаем толщину коры здесь 5 км).

Толщина коры под Гималаями по разным данным составляет 70 - 90 км. Примем, что средняя высота земной поверхности здесь составляет порядка +4 км. Тогда высота приведенного уровня мантийного вещества для района Гималайских гор составляет от -6.6 км до -9.64 км для принятых значений плотностей коры и мантии. Конечно, действительные плотности и толщины могут отличаться от принятых нами, но уточнение их значений не изменит сути наших выводов, а только уточнит рельеф приведенного уровня.

Чем обусловлено такое отличие поверхности приведенного уровня от горизонтальной? Оно образуется из-за течения очень вязкой жидкости - мантии. Ее приведенная поверхность просто не успевает стать равновесной горизонтальной, поскольку равновесие непрерывно нарушается за счет подъема из глубин более горячего и потому более легкого вещества. Стремясь к равновесию, вязкое мантийное вещество медленно течет под земной корой от возвышенностей к низинам, от места подъема к месту опускания мантийного вещества, и остывает по ходу движения под корой за счет ее теплопроводности. Так и образуется в мантии самосогласованный квазистационарный конвекционный поток. Причем разность высот приведенной поверхности (над восходящей и нисходящей частями потока) и является движущей силой конвекционного потока в вязкой мантийной жидкости. Если бы мантийная жидкость имела свободную поверхность, эта поверхность совпадала бы с вычисленной нами приведенной поверхностью, и выглядела бы она как совокупность поднятий над восходящими потоками и впадин над нисходящими.

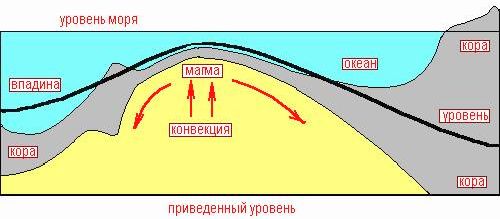
При этом поднятия поверхности приведенного уровня будут иметь горизонтальные, почти плоские вершины, поскольку на вершине восходящего потока и температура выше, и давление меньше (вязкость мантийного вещества зависит от температуры и давления). Поэтому вязкость мантийного вещества здесь меньше, и поверхность приведенного уровня практически горизонтальна на сравнительно большом участке (почти как у воды). А в зоне погружения вязкость мантийного вещества намного выше - там и температура ниже, и давление выше. Поэтому в зоне погружения вязкость мантийной жидкости может быть так велика, что мантийное вещество в ходе своего погружения не будет успевать плавно принимать равновесную форму, в результате чего в зоне нисходящего мантийного конвекционного потока возможны глубинные землетрясения с быстрым разрушением слишком твердой, хрупкой жидкости, не успевающей в ходе погружения принимать равновесную форму. Вернее, при пластических деформациях - глубинных землетрясениях будет выравниваться квазиупругая деформация сжатия аморфного (очень вязкого жидкого) вещества мантии в различных направлениях.

Мантийные конвекционные потоки самосогласованны и потому устойчивы и по конфигурации и по скоростям в масштабах миллионов и миллиардов лет. Для изменения их конфигурации необходимо изменить геометрию препятствий и размещения источников и стоков тепла. Если скорость потока слишком мала, тепло не успевает отводиться, вещество перегревается, расширяется, увеличивается перепад высот, увеличивается скорость движения и теплопереноса. Если же скорость слишком велика, температура выравнивается, уменьшается перепад высот, поток замедляется.

Сравнивая полученные высоты приведенного уровня, видим, что самую большую высоту приведенная поверхность имеет в окрестностях срединно-океанических поднятий, где велик поток глубинного тепла. То есть, здесь поднимается чуть более горячий восходящий поток мантийного вещества. Отсюда и начинается движение образующейся здесь из жидкой мантии твердой коры (и пока еще очень тонкой в этом месте) в обе стороны от линии спрединга. Такой же результат дают прямые геодезические измерения и палеомагнитные исследования. А самые низкие высоты приведенной поверхности мы обнаруживаем в зонах схождения литосферных плит (в зонах глубочайших впадин и высочайших гор). Понятно, что достаточная прочность огромных участков коры может вносить свои коррективы.

Поверхность приведенного уровня коррелирует с формой геоида - километрам отклонений приведенного уровня от среднего вверх соответствуют десятки метров отклонения геоида (уровня моря) от поверхности эллипсоида вниз. Это хорошо видно при сопоставлении карт движения литосферных плит, изолиний геоида и глубин-высот. Желательно добавить карту толщины коры. Корреляция обусловлена тем, что в зоне восходящего потока равный по высоте столб более горячего мантийного вещества имеет меньшую плотность, чем такой же столб менее горячего вещества в зоне нисходящего потока. Поэтому поверхность одинакового гравитационного потенциала (геоид) в зоне восходящего потока расположена несколько ниже, чем в зоне нисходящего потока.

Мы можем оценить некоторые параметры мантийных конвекционных потоков. Вертикальные столбы мантийного вещества под приведенными поверхностями в зоне восходящего и нисходящего потоков от поверхности до низа слоя конвекции имеют приблизительно равные веса (и массы). Поэтому по толщине слоя конвекции H и по разности высот приведенного уровня H можно вычислить разность температур T в восходящей и нисходящей частях потока, задавшись значением коэффициента температурного расширения: T = H / (H*k) = 7500м / (2 800 000м * 0.00001/1°С) 270°С. Здесь H = 2 800 000 м - толщина конвекционного слоя, k = 0.00001/1°С - линейный коэффициент температурного расширения.

Исходя из теплоемкости мантийного вещества (для базальта Сq 660 ккал/( кубич.метр * градус С)), величины теплового потока (Q = 800-8000 ккал/(год*м2)) и только что вычисленной разности температур (270°С) в восходящей и нисходящей частях потока, можно вычислить скорость V мантийного конвекционного потока, доставляющего тепло из глубин к коре (которое и наблюдается как поток глубинного тепла через поверхность коры).

Q = (Сq * Т) * V ; V = Q / ( Т * Сq) = 800-8000 (ккал/(год*м2))/(270*660) = 5-50 мм/год.

Приняв, что горизонтальное сечение конвекционного потока на 1/3 восходящее, на 1/3 нисходящее, на 1/3 неподвижное, получим скорость потока от 15 мм/год до 150 мм/год, что приблизительно совпадает со скоростью смещения литосферных плит в ходе спрединга. Для более точного определения скорости конвекционного мантийного потока нужно уточнить исходные параметры и геометрическую конфигурацию этого потока.

Отметим, что с целью более наглядного раскрытия механизма работы мантийных конвекционных потоков и вязкого увлечения ими литосферных плит (приводящего к их дрейфу) мы оставляем за рамками рассмотрения взаимно компенсирующееся адиабатическое понижение-повышение температуры при понижении-повышении давления в восходящих - нисходящих частях этих потоков и другие детали процессов, фиксируясь на главном. Подчеркнем, что движение литосферных плит обусловлено именно тем, что мантийные потоки увлекают, тянут их. Ведь если бы плиты соскальзывали по наклонной приведенной поверхности опережающими темпами (по сравнению с потоком), то они достаточно быстро заполнили бы и совсем ликвидировали впадину на этой приведенной поверхности.

Силу вязкого трения, действующую со стороны движущейся вязкой магмы на участок твердой коры шириной W = 1м, расположенный на наклонной и нижней частях поверхности приведенного уровня (усилие передается и по твердой коре от более высоко расположенных участков ко всем нижележащим), можно легко подсчитать, опираясь только на геометрию приведенной поверхности. А не на неизвестное пока значение вязкости мантийного вещества. Это возможно, поскольку в форме приведенной поверхности и проявляются вязкие свойства движущегося мантийного вещества. Причем может оказаться, что величина вязкости подкоровой магмы на разных глубинах и в различных частях конвекционного потока различна (вязкость зависит от температуры и давления, т.е., глубины расположения поверхности раздела М). О вязкости магмы под корой можно будет судить по форме поверхности приведенного уровня. Эти уточнения можно будет сделать после более точного определения формы поверхности приведенного уровня:

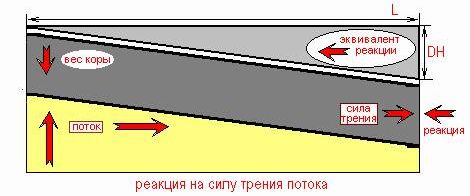
Рассмотрим рисунок, на котором изображен профиль наклонной части приведенной поверхности мантийного конвекционного потока. Здесь воздействие воображаемого тяжелого верхнего треугольника (с плотностью мантии d) компенсирует вертикальную и горизонтальную составляющие силы, действующей на кору со стороны нижележащей магмы. На самом же деле, горизонтальная составляющая (с которой кора увлекается движущейся магмой) компенсируется не действием воображаемого треугольника, а реакцией жесткой коры справа. Просто эта реакция коры эквивалентна воздействию воображаемого треугольника, а его легко подсчитать. В результате увлечения коры вязким потоком в большей части жесткой коры (почти повсеместно, за исключением вершины купола и других особенных точек, скажем в окрестностях разрыва или щели в коре) возникает напряжение сжатия, которое можно легко подсчитать.

F = g * d * W * (H)2

Правильность этого выражения подтверждается уже тем, что точно такое же выражение мы имеем для силы, действующей на боковую стенку прямоугольного сосуда, наполненного жидкостью до высоты H.

В соответствии с полученным выражением для горизонтального сжатия в зоне нисходящего потока (под Гималаями, считая линию сжатия параллельной линии спрединга) имеем: F = *9.8 (м/сек2) * 3300(кг/м3) * 1м * (7 500 м)2 = 91 * 1010 н.

Эта горизонтальная сила приложена перпендикулярно к вертикальной полосе, секущей твердую кору сверху донизу. Тогда на каждый 1м2 сечения коры (толщиной 90 км) в среднем приходится сила 1*107 н (=100кгС/см2). Это примерно 1/20 предела прочности монолитного гранита в наилучших условиях (200 МПА для одноосевого сжатия при обычной температуре). Но это в среднем. На практике же, и прочность пород из-за дефектов меньше даже при низкой температуре (в верхних слоях коры), и эффективная толщина коры меньше, и перепад высот приведенных уровней может быть больше. Кроме того, большая часть сечения коры имеет высокую температуру, отчего ее прочность существенно уменьшается. Так что эффективные напряжения одноосевого (в направлении от восходящего потока к нисходящему) сжатия в твердой коре над нисходящими частями вязкого конвекционного потока вполне достаточны для превышения предела прочности пород, составляющих кору, и выдавливания в этих зонах из коры гор (в моменты землетрясений).

Если напряжения сжатия недостаточны для преодоления предела прочности, то пластические деформации не происходят, просто кора несколько напряжена - упруго деформирована. Если же сжатие так велико, что превышается предел прочности, то в результате очередного землетрясения с очагом в некоторой точке (быстрой пластической деформации) вдоль линии сжатия, проходящей через очаг землетрясения, напряжение сжатия разряжается. Тогда как в прилегающих областях (вокруг этой линии) напряжение сжатия скачком возрастает (из-за некоторого смещения коры как целого), в результате чего может иметь место такое явление, как форшоки и афтершоки. Аналогичная картина наблюдается не только при сжатии соседних плит коры, но и при их относительном сдвиге.

Средний темп генерации гор на всей Земле за счет их выдавливания из зоны сжатия составляет: V = длина растущих гор (=60000км) * выдавливаемая часть толщины коры (=1/6Н=5км) * скорость сближения плит (=2см/год) V 6 кубических километров в год на всей Земле.

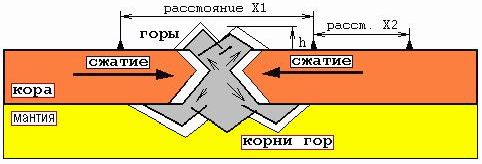 Выдавливание гор на границе плит.

Причем поперечное сечение выдавливаемого горного хребта (S=*B*h) увеличивается, в среднем, с постоянной скоростью (для Гималаев S = (1/6Н=15км) * (=2см/год) 300 м2 в год). Отсюда следует вывод, что высота гор h (при прочих равных условиях) меняется гораздо быстрее у низких гор (когда ширина основания горного хребта B мала). Если для Гималаев мы примем ширину зоны горного хребта, испытывающего поднятие в настоящее время, равной 60 км, то получим скорость роста высоты гор в этой поднимающейся зоне порядка 1 см/год, или 1 метр за 100 лет (без учета их разрушения). Отметим также, что, имея данные о скорости сближения плит, о скорости увеличения высоты гор, зная толщину коры и сечение горного хребта, легко увидеть, какая часть толщины коры выдавливается в виде гор вверх (действительно ли 1/6?), а какая - в виде корней гор вниз в ходе сближения плит.

Рекомендуем скачать другие рефераты по теме: реферат машины, реферат расчеты.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата