|
2,05
|
2,03
|
2,02
|
2,02
|
|
|
1,96
|
1,96
|
1,96
|
1,96
|
1,96
|
1,96
|
При
V < VT, считается, что разность d – случайна, т.е. при данном уровне
случайных ошибок, значения систематических незначимы. В случае V > VT
анализируют выборку на наличие членов (хі-уі) > ` d и исключают из
рассмотрения “промахи” по статистике:
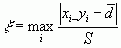 ,
, 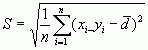 (1.6)
(1.6)
и
оценкой x по таблицам для доверительной вероятности 95% в зависимости от n
[22]. При n =20 , x £ 62,62.
Оперативная
оценка наличия "системы" в парных наблюдениях проводится графически в
координатах (x, y).
В
геолого-геофизической практике получил распространение метод выявления
систематических ошибок, состоящий в определении уравнения линейной регрессии y
на x ( x -основные геофизические, y - контрольные геологические измерения) и в
оценке существенного отличия коэффициента регрессии и свободного члена от
единицы и нуля соответственно [12, 17, 20, 21]. Однако, как показано в [26]
уравнение регрессии в общем случае не описывает зависимости между точными
результатами измерений, и, следовательно, не может быть использовано для
корректного выявления систематических ошибок. Действительно, сравнивая два ряда
измерений: основной (Xi) и контрольный (Уi), выполненные без случайных ошибок
можно записать:
Уi=a
у/х× Xi +b (1.7)
Это
уравнение определяет функциональное соотношение между точными результатами
измерений и условием отсутствия систематических ошибок является выполнение
равенств:
a
= 1, b = 0 (1.8)
В
случае опробования оба ряда отягощены случайными погрешностями, как основной, так и контрольный. Причем считается, что последний не имеет систематических
ошибок. Задача состоит в том, чтобы определить величину и значимость
систематических расхождений при заданном уровне случайных ошибок в каждом
сравниваемом ряде измерений. В этом случае связь между xi и уi может быть представлена
линейным уравнением регрессии:
уi
= a у/х× xi + ву/х (1.9)
При
этом, если s 2 (x ), s 2( e (Х)), s 2( e (У)) - дисперсии истинных содержаний и
ошибок измерений соответственно, то дисперсии результатов измерений, коэффициенты регрессии и корреляции будут равны [27]:
s
2 (х)= s 2 (x )+s 2( e (Х)), s 2 (у)= s 2 (x )+s 2( e (У)),
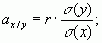
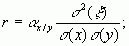 (1.10)
(1.10)
Откуда
получим:
Рекомендуем скачать другие рефераты по теме: рынок реферат, контрольные рефераты.
Предыдущая страница реферата |
1
2
3
4
5
6
7
8 |
Следующая страница реферата
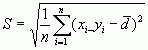 (1.6)
(1.6) Главная
Главная