Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

= (p,g,l) 

c = apy при p < c02/a2

(6)

с = с0 при p > c02/a2 

ug - ul = F(Pi) (7) 

Здесь u - скорость; - плотность; р - давление; эти величины, употребляемые без индексов, характеризуют двухфазную смесь в целом; с - содержание летучего компонента в конденсированной фазе, с0 - полное содержание летучего компонента в исходной магме; а и - постоянные, зависящие от рода магмы и диапазона давлений, для кислых и средних магм и диапазона давлений до 3-4 кбар обычно принимаются значения а=0,0013 бар-1/2, =0,5. Индексы st, u и d означают потери давления статические, динамические и диссипативные соответственно; nv - нелетучий компонент, v - летучий компонент, g - газовая фаза, l - конденсированная фаза. (3) - два уравнения непрерывности (для нелетучего и летучего компонентов); (4) - уравнение импульсов, записанное как сумма приращений потерь давления вдоль канала; (5) - три уравнения состояния (для каждой из двух фаз и для смеси), в изотермическом приближении представляющие собой выражения, связывающие плотность с давлением; (6) - закон массообмена между фазами (растворимость летучего компонента в нелетучем); (7) - характеризует распределение импульса между фа эти величины зами (Pi - различные параметры потока, от которых зависит обмен импульсом между фазами).  

В качестве граничных условий задавались давления на обоих концах канала, а также условия на границах зон с разной структурой потока. Нижняя граница пузырьковой зоны определялась условием с=с0; верхняя граница пузырьковой зоны определялась заданием объемной доли газовой фазы (обычно 0,75, что примерно соответствует плотной упаковке одинаковых пузырьков). Верхняя граница зоны частично разрушенной пены определялась моментом достижения газом, движущимся сквозь частично разрушенную пену (которая моделировалась засыпкой), скорости, достаточной для псевдоожижения пирокластических частиц. Конкретная форма уравнений различна для разных зон.

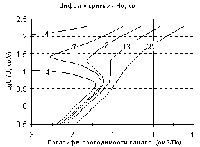
Рис. 1

 Система (3-7) решалась численным интегрированием уравнения моментов вдоль канала с вычислением всех необходимых величин с помощью остальных уравнений системы и использованием итерационной процедуры для удовлетворения граничным условиям на обоих концах канала. В результате получались величины массового расхода и различных параметров потока вдоль канала. Важным результатом являлось определение положения границ между зонами с разной структурой потока, что позволило физически объяснить связь режимов извержения с характеристиками системы.

Для анализа результатов из всех характеристик системы были выбраны три так называемых основных управляющих параметра: 1 - глубина очага (длина канала) - Н0; 2 - параметр проводимости канала =b2/, где b - характерный поперечный размер канала; 3 - давление в очаге рo, вместо которого обычно для удобства использовалось избыточное давление: pex=po-lgH0. Выбор основных управляющих параметров до некоторой степени произволен, но от того, насколько он удачен, зависит возможность быстро нащупать главные закономерности.

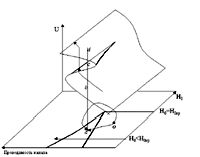
Рис. 2

 Некоторые результаты расчетов показаны на рис.1. На всех графиках ордината - скорость подъема магмы без пузырьков - величина, пропорциональная расходу; абсцисса - один из управляющих параметров, другой показан числом у каждой кривой, а третий зафиксирован. Обращает на себя внимание одинаковая форма всех графиков: в определенной области часть кривых имеет зигзагообразную форму - одному значению управляющего параметра соответствуют три значения расхода. Причем, границы области неоднозначности расхода определяются также значением одного из управляющих параметров.  

Верхняя и нижняя ветви каждой такой кривой отвечают устойчивым состояниям системы, средняя - неустойчивому. Изменение состояния системы при изменении параметра, отложенного по абсциссе, описывается движением точки вдоль устойчивой ветви соответствующей кривой. Если точка подойдет к повороту кривой на неустойчивую ветвь, дальнейшее изменение параметра в том же направлении заставит точку перескочить на другую устойчивую ветвь - система скачком перейдет в другое устойчивое состояние, очень сильно отличающееся от первого. Такой скачок называют <катастрофой", и такого рода семейства кривых возникают при математическом моделировании очень большого числа природных процессов и изучаются в так называемой теории катастроф [7] (рис.1).

Каждое семейство кривых представляет собой набор сечений некоторой поверхности, называемой многообразием катастрофы с особенностью типа <сборка". Такая поверхность показана на рис.2.  

Сборка является типичной стандартной катастрофой двупараметрических семейств функций [7], обладающей структурной устойчивостью, то есть сохраняющаяся при не очень значительных изменениях всех параметров. Эта устойчивость отвечает устойчивости режимов извержения.

Проекция сборки на плоскость управляющих параметров имеет вид угла с острием, внутри которого каждой точке плоскости отвечают три образа на поверхности многообразия катастрофы (три значения расхода), соответствующие трем листам изогнутой поверхности (рис.2). Верхний и нижний лист соответствуют устойчивым состояниям системы, средний - неустойчивым. Острие угла называется точкой сборки. Значения параметров, соответствующие координатам точки сборки, будем называть критическими - Hкр и sкр.  

Изменение значений управляющих параметров описывается движением точки по плоскости. Параметр, изменение которого проводит изображающую точку на плоскости через острие угла параллельно оси сборки, называется "расщепляющим" и определяет саму возможность неоднозначности решений. При этом движение образа точки на многообразии катастрофы, описывающее изменение расхода, возможно как по нижнему, так и по верхнему листу поверхности - точка сборки является точкой бифуркации . Параметр, проводящий изображающую точку перпендикулярно оси сборки, называется "нормальным", при его изменении пересечение границы сборки - сепаратрисы катастрофы - приводит к скачку системы из одного устойчивого состояния в другое.

Управляющих параметров нами выделено три, и сборка качественно описывает поведение системы при изменении каждой пары из них. В реальности могут изменяться все три параметра одновременно и картина будет несколько сложнее, но, в любом случае наличие сборок предопределяет скачки. Практически в процессе естественной эволюции извержения на каждом ее этапе преобладает изменение лишь одного или двух параметров, и поведение системы может быть описано простой сборкой.  

Физический механизм катастрофического скачка заключается в следующем. Рост расхода приводит к росту скорости потока на всем протяжении канала во всех зонах с разной структурой потока и, как следствие, к увеличению сопротивления, ограничивающего этот рост. Одновременно рост расхода приводит к росту протяженности зоны газовзвеси по отношению к зонам с жидкостным течением. В канале вулкана из-за высокой вязкости магмы и относительно небольшого содержания летучих отнесенное к единице длины сопротивление на участке жидкостного течения на несколько порядков превосходит соответствующее сопротивление на участке газовзвеси. Таким образом, изменение соотношения протяженностей в пользу газовзвеси уменьшает полное сопротивление канала и способствует дальнейшему увеличению расхода. В этом же направлении работает и уменьшение средней плотности вещества в канале. Если эффект увеличения расхода, вызванный увеличением зоны газовзвеси, начинает преобладать над эффектом уменьшения, вызванным ростом скорости, возникает положительная обратная связь и начинается его катастрофический рост. Этот рост может быть остановлен лишь когда жидкостная зона уменьшится настолько, что ее полное сопротивление станет близким к сопротивлению зоны газовзвеси, или на выходе канала будет достигнута критическая скорость потока (местная скорость звука). В последнем случае разработка за счет эрозии расширяющегося сопла может привести и к сверхзвуковому истечению.

Переход в экструзивную стадию или остановка извержения связаны с возникновением положительной обратной связи противоположного знака: уровень фрагментации поднимается, сопротивление растет, расход падает, что приводит к дальнейшему подъему уровня фрагментации.

Объяснение природы катастрофических эксплозивных извержений

Основное, что позволила объяснить теория - это природу, условия возникновения и механизм развития так называемых катастрофических эксплозивных извержений (КЭИ) - наиболее сильно воздействующих на окружающую среду. Такое извержение долгое время интерпретировалось как взрыв или серия взрывов (отсюда название), однако сейчас стало ясно, что оно включает много стадий, большинство которых представляет собой стационарное истечение. Полная картина КЭИ прояснилась только после детально наблюдавшегося извержения вулкана Сент Хеленс в 1980 году [18]. Его основные стадии следующие:

1. Газовая эмиссия (умеренные взрывы) с резургентной пирокластикой - продолжительность от часов до дней.

2. Умеренная эксплозивная активность с выбросом ювенильной пирокластики - от часов до лет.

Рекомендуем скачать другие рефераты по теме: оформление титульный реферата, доклад 8 класс.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата