Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Пусть в некотором объеме, занимаемом метастабильной магмой, началась спонтанная полимеризация и, следовательно, газоотделение. Образование свободной газовой фазы и рост газовых пузырьков приводит к возрастанию давления в этом объеме и снижает уровень метастабильности и, следовательно, ведет к замедлению и приостановке процессов полимеризации и газоотделения. Рост газовых пузырьков происходит до достижения ими состояния механического и химического равновесия с окружающей их магмой. После окончания роста пузырьков давление в магме постепенно приходит к первоначальному значению, и процессы полимеризации и газоотделения начинаются вновь. Скорость роста пузырьков в магме зависит от многих факторов, главные из которых: давление пересыщения магматического расплава, вязкость магмы, коэффициенты диффузии и теплопроводности. Таким образом, в магме в области спонтанной полимеризации периодически будут генерироваться импульсы давления с частотой, зависящей от вышеперечисленных факторов и определяемой внутренними свойствами магмы. Эти импульсы давления на стенках трещины формируют сейсмические волны, период колебаний в которых определяется длительностью самого импульса давления в магме и размерами трещины. 

Исходя из предлагаемой гипотезы, попытаемся связать период сейсмических колебаний ГДП землетрясений с физическими характеристиками магматического расплава и сравнить с экспериментальными данными. Для этого определим основные факторы, влияющие на рост пузырьков. 

Так как теплопроводность играет заметную роль только для больших пузырьков (а в нашем случае мы имеем дело с пузырьками микронных и субмикронных размеров), процесс роста пузырьков будем считать изотермическим. Для того чтобы определить, какому из оставшихся факторов (диффузия и вязкость) принадлежит основная роль в длительности формирования импульса давления в магме, рассмотрим влияние диффузии и вязкости на рост пузырьков в магме независимо друг от друга. Расчеты будем проводить для водонасыщенного базальтового расплава. Вначале оценим влияние вязкости. 

Решение задачи о динамике газовых пузырьков основывается на уравнении Рэлея-Тейлора c учетом вязкости [42]:

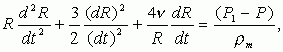(1)

где R - радиус пузырьков, m - плотность магмы, - кинематическая вязкость магмы, P - давление в магме, P1 - давление в газовом пузырьке.

Для того чтобы оценить время релаксации избыточного давления, возникающего при расширении пузырьков, пренебрегаем первыми двумя членами в уравнении (1) вследствие их малости:

(2)

Условие механического равновесия в газовом пузырьке будет определяться уравнением:

(3)

где - коэффициент поверхностного натяжения.

Подставляя выражение (3) в (2), получим уравнение:

,

из которого интегрированием по времени можно определить длительность импульса:

=. (4) 

Для водонасыщенных базальтовых магм на глубине 20 - 40 км по данным [18] вязкость = m ~ 101 -102 Пуаз (1-10 Па/с), а 102 дин/см (10-1 Па/c) [17]. Как следует из формулы (4), для ~ 1с радиус R возникших в магме пузырьков должен составлять 10-1-10-2см, что на несколько порядков превосходит расчетные [20] и экспериментальные [43] данные. Следовательно, время в нашей модели должно определяться другими параметрами.

Рассмотрим теперь процесс роста пузырьков газа исходя из уравнения диффузии:

(5)

где D - коэффициент диффузии, (для базальтовой магмы Ключевского вулкана при P = 5000 атм ( 5.108 Па ) D ~ 10-9 м2/c [16]); dM - масса газа, диффундирующего в пузырек за время dt через поверхность пузырька ds; d g/dx - градиент концентрации свободного газа в магме, равный:

где W(P) - весовая концентрация растворенного в магме газа, dW(P)/dP 4*10-10 г/ Па [16].

Из уравнения (5) следует, что длительность импульса в магме будет зависеть от коэффициента диффузии и концентрации свободного газа в магме по формуле:

. 

Для наших оценок о влиянии диффузии на рост пузырьков в первом приближении будем считать, что d g/dx = const и, учитывая, что dM= 4/3 R3 d , - плотность газа в пузырьках, а ds=4 R2 , из последнего уравнения получим, что:

(6)

Рекомендуем скачать другие рефераты по теме: налоги и налогообложение, конспект по русскому.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата