
Природа и механизм резких изменений режима вулканических извержений
| Категория реферата: Рефераты по геологии
| Теги реферата: шпаргалка рф, контрольные за 1 полугодие
| Добавил(а) на сайт: Латушкин.
Предыдущая страница реферата | 1 2
![]() =
= ![]() (p,
(p,![]() g,
g,![]() l)
l)
c = apy при p < c02/a2
(6)
с = с0 при p > c02/a2
ug - ul = F(Pi) (7)
Здесь
u - скорость; ![]() -
плотность; р - давление; эти величины, употребляемые без индексов, характеризуют двухфазную смесь в целом; с - содержание летучего компонента в
конденсированной фазе, с0 - полное содержание летучего компонента в
исходной магме; а и
-
плотность; р - давление; эти величины, употребляемые без индексов, характеризуют двухфазную смесь в целом; с - содержание летучего компонента в
конденсированной фазе, с0 - полное содержание летучего компонента в
исходной магме; а и ![]() -
постоянные, зависящие от рода магмы и диапазона давлений, для кислых и средних
магм и диапазона давлений до 3-4 кбар обычно принимаются значения а=0,0013 бар-1/2,
-
постоянные, зависящие от рода магмы и диапазона давлений, для кислых и средних
магм и диапазона давлений до 3-4 кбар обычно принимаются значения а=0,0013 бар-1/2, ![]() =0,5.
Индексы st, u и d означают потери давления статические, динамические и
диссипативные соответственно; nv - нелетучий компонент, v - летучий компонент, g - газовая фаза, l - конденсированная фаза. (3) - два уравнения непрерывности
(для нелетучего и летучего компонентов); (4) - уравнение импульсов, записанное
как сумма приращений потерь давления вдоль канала; (5) - три уравнения
состояния (для каждой из двух фаз и для смеси), в изотермическом приближении
представляющие собой выражения, связывающие плотность с давлением; (6) - закон
массообмена между фазами (растворимость летучего компонента в нелетучем); (7) -
характеризует распределение импульса между фа эти величины зами (Pi
- различные параметры потока, от которых зависит обмен импульсом между фазами).
=0,5.
Индексы st, u и d означают потери давления статические, динамические и
диссипативные соответственно; nv - нелетучий компонент, v - летучий компонент, g - газовая фаза, l - конденсированная фаза. (3) - два уравнения непрерывности
(для нелетучего и летучего компонентов); (4) - уравнение импульсов, записанное
как сумма приращений потерь давления вдоль канала; (5) - три уравнения
состояния (для каждой из двух фаз и для смеси), в изотермическом приближении
представляющие собой выражения, связывающие плотность с давлением; (6) - закон
массообмена между фазами (растворимость летучего компонента в нелетучем); (7) -
характеризует распределение импульса между фа эти величины зами (Pi
- различные параметры потока, от которых зависит обмен импульсом между фазами).
В качестве граничных условий задавались давления на обоих концах канала, а также условия на границах зон с разной структурой потока. Нижняя граница пузырьковой зоны определялась условием с=с0; верхняя граница пузырьковой зоны определялась заданием объемной доли газовой фазы (обычно 0,75, что примерно соответствует плотной упаковке одинаковых пузырьков). Верхняя граница зоны частично разрушенной пены определялась моментом достижения газом, движущимся сквозь частично разрушенную пену (которая моделировалась засыпкой), скорости, достаточной для псевдоожижения пирокластических частиц. Конкретная форма уравнений различна для разных зон.
|
|
|
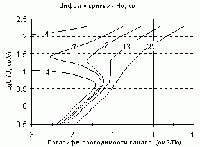
Рис. 1 |
Система (3-7) решалась численным интегрированием уравнения моментов вдоль канала с вычислением всех необходимых величин с помощью остальных уравнений системы и использованием итерационной процедуры для удовлетворения граничным условиям на обоих концах канала. В результате получались величины массового расхода и различных параметров потока вдоль канала. Важным результатом являлось определение положения границ между зонами с разной структурой потока, что позволило физически объяснить связь режимов извержения с характеристиками системы.
Для
анализа результатов из всех характеристик системы были выбраны три так
называемых основных управляющих параметра: 1 - глубина очага (длина канала) - Н0;
2 - параметр проводимости канала ![]() =b2/
=b2/![]() , где b - характерный поперечный размер канала; 3 - давление в очаге рo, вместо которого обычно для удобства использовалось избыточное давление: pex=po-
, где b - характерный поперечный размер канала; 3 - давление в очаге рo, вместо которого обычно для удобства использовалось избыточное давление: pex=po-![]() lgH0.
Выбор основных управляющих параметров до некоторой степени произволен, но от
того, насколько он удачен, зависит возможность быстро нащупать главные
закономерности.
lgH0.
Выбор основных управляющих параметров до некоторой степени произволен, но от
того, насколько он удачен, зависит возможность быстро нащупать главные
закономерности.
|
|
|
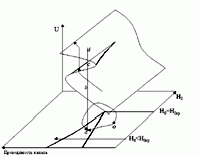
Рис. 2 |
Некоторые результаты расчетов показаны на рис.1. На всех графиках ордината - скорость подъема магмы без пузырьков - величина, пропорциональная расходу; абсцисса - один из управляющих параметров, другой показан числом у каждой кривой, а третий зафиксирован. Обращает на себя внимание одинаковая форма всех графиков: в определенной области часть кривых имеет зигзагообразную форму - одному значению управляющего параметра соответствуют три значения расхода. Причем, границы области неоднозначности расхода определяются также значением одного из управляющих параметров.
Верхняя
и нижняя ветви каждой такой кривой отвечают устойчивым состояниям системы, средняя - неустойчивому. Изменение состояния системы при изменении параметра, отложенного по абсциссе, описывается движением точки вдоль устойчивой ветви
соответствующей кривой. Если точка подойдет к повороту кривой на неустойчивую
ветвь, дальнейшее изменение параметра в том же направлении заставит точку
перескочить на другую устойчивую ветвь - система скачком перейдет в другое
устойчивое состояние, очень сильно отличающееся от первого. Такой скачок
называют
Скачали данный реферат: Абоимов, Винтухов, Петра, Мосенцев, Nikitaev, Болтоногов, Anoshkin.
Последние просмотренные рефераты на тему: тезис, сочинение, курсовая работа, школьные рефераты.
Категории:
Предыдущая страница реферата | 1 2
 Главная
Главная