Предыдущая страница реферата | 1  2

где - упругие перемещения стенки плотины, зависящие только от координаты .  

Собственные колебания грунтовой плотины с учетом водной среды водохранилища представляют собой упорядочное движение грунтовой плотины, протекающее при отсутствии внешних воздействий. Решение проблемы заключается в следующем: ищется нетривиальное решение уравнения (4)  при однородных кинематических условиях в виде (5).

Постановка (8) в (4) сводит данную задачу к действительной вариационной задаче о собственных значениях в виде

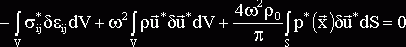                 (9)

                                           ,                        

где - амплитуда напряжений, - искомая собственная частота и форма колебаний плотины с учетом водной среды, - гидродинамическое давление воды на стенку плотины, которое имеет вид

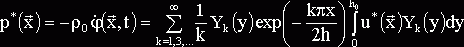            (10)

При этом для решения вариационной задачи (9) используется закон Гука, геометрические соотношения Коши (7) и стандартная процедура МКЭ с использованием треугольного конечного элемента с линейной аппроксимацией поля перемещений внутри элемента.

При этом для i-го узла n-го конечного элемента первые вариации работ упругих, инерционных сил и гидродинамического давления относительно ui будут иметь вид

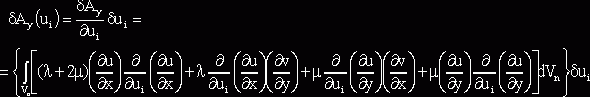
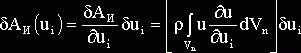            ,                                                 (11)

,

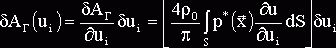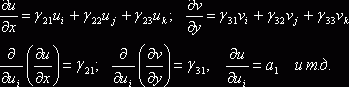
Здесь l, m - константы Ламе, r, r0- плотность материала сооружений и воды.

После интегрирования этих выражений получим строки матриц жесткости, массы и присоединённой массы воды, соответствующие перемещениям ui для n-го элемента. Если эти операции повторить для узлов j и k, а также для перемещения v, то мы получим матрицы жесткости и массы порядка 6´6 для n-го конечного элемента и соответствующие матрицы масс от воды к узлам конечного элемента (если эти узлы соприкасаются с водой). Таким образом, сформировав для каждого конечного элемента свою матрицу [K], [M], [Mв] и объединив их, получим алгебраическую задачу на собственные значения для рассматриваемого сооружения с учетом взаимодействия с водой:

    ,                                       (12)

где [K]-матрица жесткости плотины, [Mc]=[M]+[Mв] - суммарная матрица массы плотины и массы воды, w и {u} - искомые собственная частота и собственный вектор плотины, взаимодействующей с водой.  

Решая уравнение (12) методом Мюллера и квадратного корня определим собственную частоту и форму колебания гидроупругой системы “грунтовая плотина с водой”. Такая постановка и методика решения задачи о собственных колебанях гидроупругих систем позволяют получить, в отличие от известных работ, более реальную картину динамики системы.

С помощью изложенного выше алгоритма исследованы собственные колебания грунтовых плотин, взаимодействующих с водной соедой.

Анализ полученных результатов позволяет сделать вывод о том, что учет взаимодействия воды с плотиной приводит  к уменьшению частот собственных колебаний и для первых восьми частот составляет от 2 до 10% в зависимости от вида плотины.  Эти отклонения зависят от многих  факторов: от высоты плотины,  характера форм колебаний сооружения, а также от значения коэффициента откоса, контактирующего с водой. При этом самым значимым фактором является крутизна верхового откоса, определяемая коэффициентом откоса - с увеличением коэффициента откоса соответственно уменьшается влияние воды на динамические характеристики плотины. Для вертикальной стенки значение гидродинамического давления воды является определяющим.

Список литературы

1. Кульмач П.П. Гидродинамика гидротехнических сооружений (Основные плоские задачи). -М.: Изд-во АН СССР. –1963. 190 с.

2. Шульман С.Г. Расчеты сейсмостойкости гидросооружений с учетом влияния водной среды. М.: Энергия, 1976. 336 с.

Скачали данный реферат: Ярмолинский, Кочинян, Mar'ina, Киприянов, Яблочкин, Малинья, Баженов.
Последние просмотренные рефераты на тему: реферат на тему орган, сообщение об открытии, предмет культурологии, скачать сообщение.





Предыдущая страница реферата | 1  2