Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

При этом каждая цифра ai < li, а каждый i-ый разряд имеет весовой коэффициент:

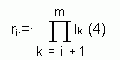
В работе В.И. Амелькина[5] сформулирована теорема существования и единственности такого разложения.

Использование полиадической системы счисления позволяет построить следующий алгоритм упаковки. Пусть задана целочисленная матрица A=ai,j , i=1,..,m, j=1,..,n.

С помощью преобразования

где

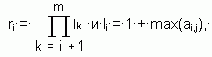
эту матрицу можно заменить двумя векторами N=nj и L=li, причем существует обратное преобразование

ai,j = [ nj / ri ] - [ nj / (lj*ri) ] * li , (6)

позволяющее по N и L восстановить любой элемент ai,j с погрешностью E=0. (Квадратными скобками здесь обозначена операция выделения целой части). Так как для хранения векторов N и L требуется меньше двоичных единиц, чем для хранения исконой матрицы, коэффициент сжатия

оказывается больше единицы. Здесь So- число двоичных единиц, требуемых для хранения исходной матрицы, Si- число двоичных единиц, требуемых для хранения элементов векторов N и L.

Как показали приведенные нами численные эксперименты, описанный выше алгоритм не обладает высокой эффективностью. К его недостаткам можно также отнести сложности, возникающие при реализации программ- упаковщиков на его основе.

В этой связи, мы поставили перед собой задачу совершенствования описанного алгоритма с целью повышения его эффективности и создания таких его версий, которые легко реализовывались бы в виде программ.

В нашем алгоритме кодируемая информация представляется в виде множества значений переменных байтового типа. Значения объединены в группы по четыре числа. Пусть таких групп в исходном информационном массиве выделено m (m>>4).

Выполнив для указанного массива описанную выше процедуру кодирования, получим два вектора - N с m элементами и L, состоящий из 4-х элементов.

Для повышения эффективности алгоритма (а под эффективностью мы здесь и в дальнейшем понимаем, в первую очередь, повышение коэффициента сжатия), выполним следующее преобразование.

Каждый из элементов полученного вектора N представим в виде 4-х разрядного двухсотпятидесятишестиричного числа и к полученной 4-х строчной матрице вновь применим процедуру полиадиического кодирования.

Многократно повторив описанную последовательность шагов, можно существенно повысить коэффициент сжатия исходной информации. В приведенных ниже таблицах показаны этапы сжатия исходной информации, представляющей собой некоторый набор латинских литер.

Таблицы рассчитывались с помощью табличного процессора из интегрированного пакета Works 2.0.

Приведенный пример подтверждает высокую эффективность описанного алгоритма.

Очевидно также, что на базе описываемого подхода могут быть реализованы быстрые и эффективные программы-упаковщики.

Таблица 1. Пример нумерационного кодирования

Исходный массив Компоненты вектора L 

Рекомендуем скачать другие рефераты по теме: сочинение 7 класс, конспект урока в школе.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата