Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

5. Расщепить вершину в соответствии с цветами контактов.

6. Создать вертикальное соединение для доглега, если это возможно, и вернуться на шаг 1.

Рассмотрим отдельные шаги алгоритма более детально. На шаге 2 для каждой итерации выбирается критическая вершина в VCG. Критерием выбора является значение следующей функции:

 f = cyclesa * width-b * priority-g , где

cycles - количество циклов, проходящих через данную вершину,

width - ширина, priority - приоритет соответствующей цепи,

a > 0, b ³ 0, g ³ 0 - коэффициенты важности перечисленных параметров, которые выбираются пользователем в зависимости от конкретной задачи.

Определенная таким образом функция выбора позволяет расщеплять большее количество циклов за одну итерацию, выбирать для доглега цепи меньшей ширины, а также не усложнять конфигурацию приоритетных цепей, например цепей земли/питания.

На шаге 3 для найденной критической вершины a строится расширенный граф вертикальных ограничений (Expanded Vertical Constraints Graph) следующего вида: EVCGa = ((X a)?Ka, Ua), где X - множество вершин исходного VCG, a - критическая вершина VCG, Ka - множество новых вершин, образованных контактами сегмента, соответствующего вершине a, Ua - множество ориентированных ребер, соединяющих новые вершины с другими вершинами VCG. Такой граф содержит более детальную информации о циклах, проходящих через критическую вершину. На рисунке 3 приведен пример EVCGa для канала, показанного на рисунке 2.

На шаге 4 строится локальный граф контактов для критической вершины a (Local Pin Graph): LPGa = (Ka, Va), где Va - множество неориентированных ребер. Ребро vi?Va соединяет вершины km, kn ? Ka, если в графе EVCGa существует путь между вершинами km и kn.  Локальный граф для вершины a изображен на рисунке 3.

Каждое ребро локального графа контактов соответствует как минимум одному циклу, проходящему через критическую вершину VCG, и указывает на контакты, образующие этот цикл. Таким образом, если ребро существует между парой вершин локального графа, то соответствующие им контакты должны быть назначены в различные группы при расщеплении вершины VCG. В этом случае соответствующие ребру циклы будут удалены.

Возможен случай, когда в локальном графе появляется петля. Петля не может быть удалена путем разбиения контактов на группы, так как  контакт не может быть расщеплен на части. В этом случае проходящий через вершину цикл не может быть удален путем расщепления только данной вершины.

Использование локального графа контактов позволяет свести задачу разбиения контактов на группы к задаче раскраски неориентированного графа. Необходимо раскрасить локальный граф контактов в минимальное число цветов так, чтобы вершины, соединенные ребром, оказались раскрашены в разные цвета. Раскраска графа в минимальное число цветов будет соответствовать разбиению сегмента на минимальное число частей, достаточное для удаления циклов в VCG. Необходимо отметить, что, несмотря на сложность задачи раскраски произвольного графа в минимальное число цветов, для данного случая задача всегда может быть решена методом полного перебора, так как размерность локального графа контактов определяется числом контактов в цепи и для сигнальных цепей обычно не превышает 5.

Если локальный граф контактов не содержит нечетных циклов, то, по теореме Кенига [6], он может быть раскрашен в два цвета. В этом случае достаточно бинарного доглега. В остальных случаях требуется мульти-доглег. Пример раскраски локального графа контактов для вершины а показан на рисунке 3.

Граф вертикальных ограничений после одной процедуры мульти-доглега изображен на рисунке 3. Критическая вершина a расщеплена на три новые вершины (a’, a’’, a’’’) в соответствии с раскраской графа LPGa, а ребра, относящиеся к a, построены заново для трех новых вершин.

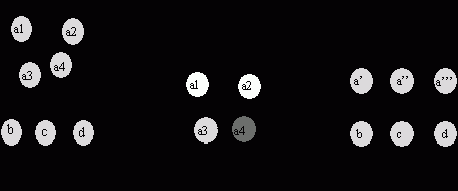
Рис.3.

Чтобы завершить процедуру мульти-доглега, необходимо найти место для вертикального соединения между новыми сегментами. Эта задача решается на шаге 7 в соответствии с [5].

В общем случае итерации повторяются до тех пор, пока не будут удалены все циклы. Граф, рассмотренный в нашем примере, был приведен к ациклическому виду за один шаг. После этого была решена задача укладки горизонтальных сегментов в канале. Результат канальной трассировки показан на рисунке 4. Необходимо отметить, что это решение не удается получить ранее известными методами.

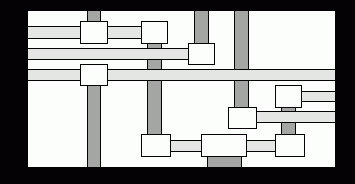
Рис.4.

Алгоритм мульти-доглега был реализован на языке С++. На рис. 5 представлен пример канала, который является сложным для задачи удаления циклов. Контакты фиксированы на верхней и нижней и упорядочены на левой и правой сторонах, VCG содержит 33 цикла. Алгоритм мульти-доглега удаляет циклы в этом примере за 9 итераций.

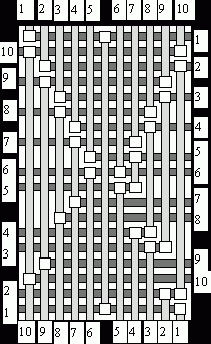
Рис.5.Трассировка сложного примера

Разработанный алгоритм приведения VCG к ациклическому виду обеспечивает, в отличие от известных алгоритмов, трассировку многослойных каналов с контактами, расположенными на любой стороне и в любом коммутационном слое, что является в настоящее время необходимым технологическим условием применения САПР СБИС.

Рекомендуем скачать другие рефераты по теме: решебник мордкович, сочинение сказка.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата