Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

В данной работе в качестве блока сжатия информации смоделирован многоканальный сигнатурный анализатор.

1.4. Принципы генерирования случайных и псевдослучайных последовательностей.

В задачах активных экспериментальных исследований современных сложных технических систем с применением статистических методов важное место принадлежит генерированию сигналов возбуждения.[4] Диктуется это не только необходимостью подачи на объект требуемого числа воздействий с заданными свойствами, но и максимальной скорости их выработки. Одним из наиболее распространённых в настоящее время методов формирования таких процессов является преобразование сигналов, получаемых с помощью так называемых генераторов белого шума (ГБШ). В применении к цифровым методам генерирования под белым шумом понимается последовательность некоррелированных чисел или цифр, распределённых, как правило, по равномерному закону.

Известны два основных метода получения цифрового белого шума: физический - генерирование случайных двоичных чисел с помощью специальных устройств - генераторов случайных чисел (ГСЧ); математический - формирование псевдослучайных числовых последовательностей (ПСЧП) по специальным программам или с использованием генераторов псевдослучайных чисел (ГПСЧ).

Принцип действия ГСЧ состоит в преобразовании случайного сигнала на выходе физического источника шума в импульсную последовательность с вероятностью появления импульса p(1)=0,5.

Общими и наиболее существенными недостатками, затрудняющими применение ГСЧ, являются ограниченное быстродействие, определяемое первичным аналоговым источником шума; низкая стабильность основных вероятностных характеристик, объясняемая нестабильностью первичных источников, дрейфом параметров преобразующих схем, источников питания и др., что требует периодической статистической проверки качества генерируемой последовательности; сложность аппаратурной реализации, вызываемая наличием нескольких источников питания; невозможность воспроизведения и предсказания генерируемых последовательностей в силу их случайной природы и т.д.

Указанные недостатки физических ГСЧ явились причиной всё более широкого распространения математических методов получения шумовых числовых последовательностей. Мгновенные значения таких псевдослучайных последовательностей в отличие от случайных в принципе могут быть предсказаны заранее. В то же время все оценки статистических характеристик конкретной реализации ПСЧП совпадают с оценками соответствующей ей случайной выборки. Любую статистическую характеристику псевдослучайной числовой последовательности можно получить, используя реализацию длиной в один период повторения ПСЧП. Для истинно случайной последовательности это потребовало бы бесконечно большую длину реализации. Искусственное увеличение периода ПС - сигнала неограниченно приближает его структуру к структуре одной из возможных реализаций истинно случайного процесса. Однако и при ограниченных величинах периода в определённых условиях псевдослучайные числовые последовательности могут заменить случайные. При анализе псевдослучайной реализации равной или меньшей длине периода вообще практически невозможно определить, является ли она отрезком регулярной или случайной последовательности. С другой стороны, если записать конкретную случайную реализацию на каком-либо носителе, и периодически воспроизводить её, то получим регулярную ПСЧП.

Таким образом, с точки зрения реальных характеристик трудно установить границу между случайными и псевдослучайными числовыми последовательностями. В то же время применение ПСЧП имеет ряд существенных преимуществ: периодический характер псевдослучайного сигнала обуславливает низкий уровень дисперсии оценок, получаемых при усреднении в течение целого числа периодов; характеристики ПСЧП абсолютно стабильны и определяются алгоритмом формирования псевдослучайных чисел; последовательность можно повторить с любого желаемого участка реализации, для чего не требуется сложных запоминающих устройств и др.

Работу генератора М-последовательности, сумматоры по модулю два которого включены в межразрядные связи, а порождающий полином равен M(x)= 11x2x2...mxm, можно описать выражением

AM(k)=VMAM(k-1),

где m-мерные вектора AM(k)=(a1M(k), a2M(k),..., amM(k)) и AM(k-1)= =(a1M(k-1), a2M(k-1),..., amM(k-1)) определяют состояния РС генератора в k-й и (k-1)-й такты работы соответственно, а матрица VM, описывающая структуру генератора, имеет вид:

 0 0 0 . . . 0 1

1 0 0 . . . 0 1

VM= 0 1 0 . . . 0 2

. . . . . . . .

0 0 0 . . . 1 m-1

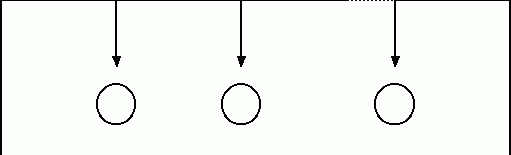
Структурная схема генератора М - последовательности, построенного по способу включения сумматоров в межразрядные связи регистра сдвига представлена на рис.1.2.

1 2 m-1

 a1(k) a2(k)  a3(k)  am(k)

Рис.1.2. Генератор М - последовательности с сумматорами по модулю два,

стоящими в межразрядных связях регистра сдвига:

Можно показать [5], что между состояниями AM(k) и A(k) РС генераторов обоих типов при AM(0)= A(0)=1000...0 существует зависимость, определяемая соотношением:

a1M(k) m m-1 m-2 . . . 2 1 a1(k)

a2M(k) 0 m m-1 . . . 3 2 a2(k)

Рекомендуем скачать другие рефераты по теме: организация диплом, древния греция реферат.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата