Динамические структуры данных: двоичные деревья

Дерево — это совокупность элементов, называемых узлами (при этом один из них определен как корень), и отношений (родительский–дочерний), образующих иерархическую структуру узлов. Узлы могут являться величинами любого простого или структурированного типа, за исключением файлового. Узлы, которые не имеют ни одного последующего узла, называются листьями.

В двоичном (бинарном) дереве каждый узел может быть связан не более чем двумя другими узлами. Рекурсивно двоичное дерево определяется так: двоичное дерево бывает либо пустым (не содержит ни одного узла), либо содержит узел, называемый корнем, а также два независимых поддерева — левое поддерево и правое поддерево.

Двоичное дерево поиска может быть либо пустым, либо оно обладает таким свойством, что корневой элемент имеет большее значение узла, чем любой элемент в левом поддереве, и меньшее или равное, чем элементы в правом поддереве. Указанное свойство называется характеристическим свойством двоичного дерева поиска и выполняется для любого узла такого дерева, включая корень. Далее будем рассматривать только двоичные деревья поиска. Такое название двоичные деревья поиска получили по той причине, что скорость поиска в них примерно такая же, что и в отсортированных массивах: O(n) = C • log2n (в худшем случае O(n) = n).

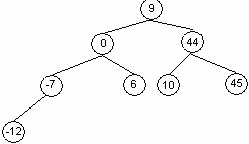
Пример. Для набора данных 9, 44, 0, –7, 10, 6, –12, 45 построить двоичное дерево поиска.

Согласно определению двоичного дерева поиска число 9 помещаем в корень, все значения, меньшие его — на левое поддерево, большие или равные — на правое. В каждом поддереве очередной элемент можно рассматривать как корень и действовать по тому же алгоритму. В итоге получаем

Выделим типовые операции над двоичными деревьями поиска:

добавление элемента в дерево;

удаление элемента из дерева;

обход дерева (для печати элементов и т.д.);

поиск в дереве.

Поскольку определение двоичного дерева рекурсивно, то все указанные типовые операции могут быть реализованы в виде рекурсивных подпрограмм (на практике именно такой вариант чаще всего и применяется). Отметим лишь, что использование рекурсии замедляет работу программы и расходует лишнюю память при её выполнении.

Пусть двоичное дерево поиска описывается следующим типом

Type BT=LongInt; U = ^BinTree; BinTree = Record Inf : BT; L, R : U End;

Покажем два варианта добавления элемента в дерево: итеративный и рекурсивный.

{Итеративный вариант добавления элемента в дерево, Turbo Pascal}

Procedure InsIteration(Var T : U; X : BT);

Var vsp, A : U;

Begin

   New(A); A^.Inf := X; A^.L:=Nil; A^.R := Nil;

   If T=Nil Then T:=A

               Else Begin vsp := T;

                         While vsp Nil Do

                          If A^.Inf < vsp^.Inf

                          Then

Рекомендуем скачать другие рефераты по теме: бесплатно ответы, управление реферат.





1  2  3  4  5  6  7 | Следующая страница реферата