|
|qdЛ
|
2qrH
|
3qrH
|
4qrH
|
5qrH
|
6qrH
|
7qrH
|
8qrH
|
9qrH
|
0qrЛ
|
1qrЛ
|
Рис.4. Машина
Тьюринга для U((n)1)=(n)10
Оценим
сложность этого алгоритма. В начале работы каретка пройдет (n-1) символ при
движении влево и (n-1) символ при движении обратно, т.е. 2(n-1). На втором
проходе - 2(n-2) и т.д. Отсюда число пройденных палочек, а следовательно и
выполненных команд будет равно n(n-1). Машина n раз выполнит команду, увеличения текущей цифры на 1. Количество просмотров цифр будет равно  ([log10n]+1)([log10n]).Таким образом, получаем
([log10n]+1)([log10n]).Таким образом, получаем
n(n-1)+n+[log10n]× ([log10n]+1) @ n2+[log10n(log10n+1)]
Пример 4.
Построить машину Тьюринга, для сравнения двух чисел a и b, заданных в унарной
форме.
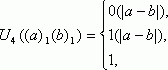 если
если 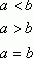
Пусть на ленте
числа a и b заданы в унарной форме. Каретка располагается над лентой так, как
показано на рисунке 5,

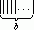
Рис.5.
b, если только в записи b, то a
TD width=106 style='width:79.85pt;border-left:none;border-top:none;border-right:solid windowtext .75pt;border-bottom:solid windowtext .75pt'
P style='margin-top:6.0pt'FONT style='font-size:10.0PT'FONT style='color:black;font-size:12.0pt'|qSUBa>bH

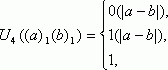 если
если  Главная
Главная