Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Если при оптимизации по критерию F1 не удается найти такого решения при котором у всех ребер ui Î G, соответствующие им сi имеют положительные значения, то оптимизация по критерию F2 минимизирует число таких ребер. Это делается из следующих соображений: чтобы обеспечить 100% реализацию (разводки) соединений, потребуется меньшее число деформаций областей или границ.

Обозначим через j число ребер всех цепей, для которых выбранные и реализованные варианты соединений включают ребра ui графа G с отрицательными значениями сi.

Пусть Nd – общее число ребер всех максимальных связывающих деревьев.

Введем третий критерий оптимизации: F3=Nd - j

Цель оптимизации заключается в максимизации F3. Это обеспечивает минимальное число соединений, требующих перетрассировки, т.е. оптимизация по F3 уменьшает число перетрассируемых соединений. Если при оптимизации по F1, имеются ребра с отрицательными сi, то в зависимости от метода дотрассировки, деформации областей или границ, используется критерий F2 или F3.

3. Разработка генетических процедур для задачи глобальной трассировки

3.1. Кодирование и декодирование хромосом

Для решения задачи глобальной трассировки  используются генетические методы оптимизации. Представим решение в виде хромосомы.  Кодирование осуществляется следующим образом. Хромосома состоит из генов. Количество генов в хромосоме Hi равно количеству ребер минимальных связывающих деревьев для всех цепей, расположенных на КП. Значением гена является номер варианта из заданного набора вариантов маршрутов, связывающих на графе G соответствующие вершины.

Например, дано КП, на котором расположено множество цепей Т = {t1, t2, t3} , рис. 2.

      

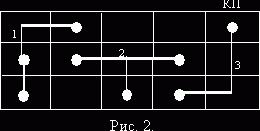
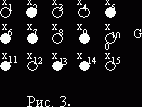
Так как мы используем графовую модель, то КП можно представить соответственно рис. 3.

Для цепи t1 множество связуемых вершин – Х1 = {x6, x2, х11}. Для цепи t2 множество связуемых вершин – Х2 = {x7, x9, x13 }. Для цепи t3 множество связуемых вершин – Х3 = {x5, x14}. С помощью алгоритма Прима для каждой цепи строится минимальное связывающее дерево МСД. Для каждой из цепей это выглядит так:рис. 4.

После этого для каждого ребра rij МСД формируется набор вариантов маршрутов, связывающих на графе G соответствующие вершины.

Ребро г11 (то есть первое ребро МСД для цепи 1) имеет два варианта прохождения маршрута r11 = {v111, v112}:  v111={x6,x1,x2}, v112={x6,x7,x2}.

Ребро r12 (второе ребро цепи 1) имеет один вариант V121={x6,x11}

Ребро г21 (то есть первое ребро МСД для цепи 2) имеет два варианта прохождения маршрута   r21={v211,v212} : v211={x7,x8,x13}   v212={x7,x12,x13}.

Ребро r22 имеет два варианта v221={x13,x8,x9}, v222={x13,x14,x9}.

Ребро г31 (то есть первое ребро МСД для цепи 3) имеет три варианта прохождения маршрута, r31 = {v311, v312, v313}, v311={x5,x10,x9,x14}; v312={x5,x4,x9,x14}; v313={x5,x10,x15,x14}.

Для решения представленного на рис. 2. структура хромосомы имеет вид рис. 5

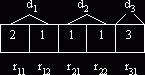
Рис. 5

Число генов равно 5. Гены g1 и g2 соответствуют ребрам r11 и  r12 дерева D1; g3 и g4 соответствуют ребрам r21 и  r22 дерева D2; g5 соответствует ребру r31  дерева D3. Значение g1 равно 2, т.к. для реализации r11 выбран вариант V112.  g2 равно 1, т.к. r12 реализован  вариантом V121.  Аналогично, т.к. r21,r22 и r31 реализованы соответственно вариантами V211, V221 и V313, то g3=1, g4=1, g5=3.

Отметим, что между структурой и видом хромосомы с одной стороны и решением (распределением соединений на КП) с другой стороны существует взаимно - однозначное соответствие. Отличительной особенностью предложенной структуры хромосомы является то, что отсутствует какая либо зависимость между генами, обусловленная самой структурой. Это свойство исключает возможность появления нелегальных хромосом, подобно тому, как это происходит с хромосомами, представляющими собой списковые структуры. В свою очередь это упрощает реализацию рассматриваемых ниже генетических операторов.   

Пусть L – число всех ребер всех МСД. L= число выводов – число цепей. Тогда объем V1 ОЗУ, необходимой для хранения информации об вариантах реализации ребер МСД, будет  , где nv – число вариантов реализации одного ребра.

Объем V2 ОЗУ необходимый для одной хромосомы  . К2 помимо всего прочего учитывает необходимость хранения фитнесса хромосомы.

Для популяции состоящей из М хромосом .

Таким образом, общий объем памяти имеет линейную зависимость и при заданных параметрах nv и M пространственная сложность алгоритма ~ O(L).

Рекомендуем скачать другие рефераты по теме: тема здоровый образ жизни реферат, банк рефератов бесплатно.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата