Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Рис. 13.8. Построение графика функции явно заданной отдельными точками.

Во втором примере рис. 13.8 показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками.

Читателю предлагается совместить самому оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.

13.2.7. Построение графиков функций, заданных их именами

Способность Maple V к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения системы, на что уходят увы не дни, а месяцы, а то и годы. Применительно к графике одной их таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках. Такую возможность наглядно демонстрирует рис. 13.9.

Этот пример показывает, что возможно построение графиков функций даже без применения в команде plot указателей масштабов. При этом масштаб по горизонтальной оси устанавливается равным по умолчанию -10..10, а по вертикальной оси устанавливается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной — условно х.

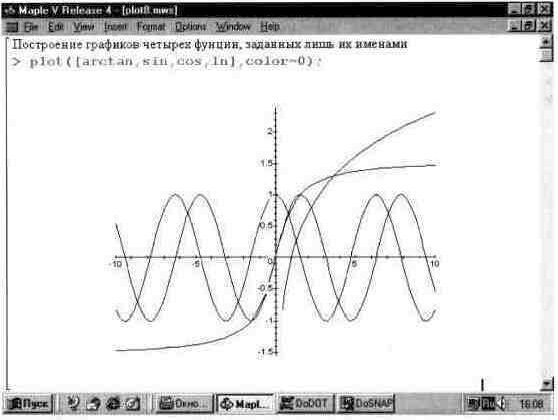
Рис. 13.9. Построение графиков четырех функции, заданных только их именами.

13.2.8. Построение графиков функции с ординатами, заданными вектором

Часто возникает необходимость построения графика точек, ординаты которых являются элементами некоторого вектора. Обычно при этом предполагается равномерное расположение точек по горизонтальной оси.

Пример построения такого графика дан на рис. 13.10.

Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет. Так что фактически строится график зависимости ординат точек от их порядкового номера п.

13.2.9. Построение графиков функций, заданных процедурами

Некоторые виды функций, например кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется рис. 13.11.

Здесь, пожалуй, полезно обратить внимание на то, что когда в функции plot указывается имя процедуры без списка ее параметров, то указатель масштаба должен просто указывать пределы графических построений по оси х.

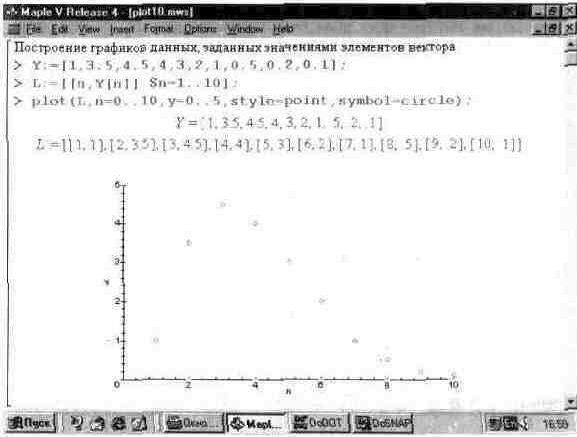
Рис. 13.10. Построение графика точек с ординатами, заданными элементами вектора.

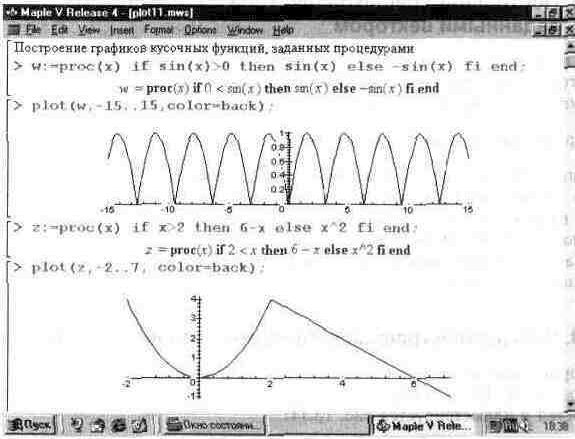
Рис. 13.11. Построение графика функций, заданных процедурами

13.2.10. Построение графиков функций, заданных функциональными операторами

Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется рис. 13.12.

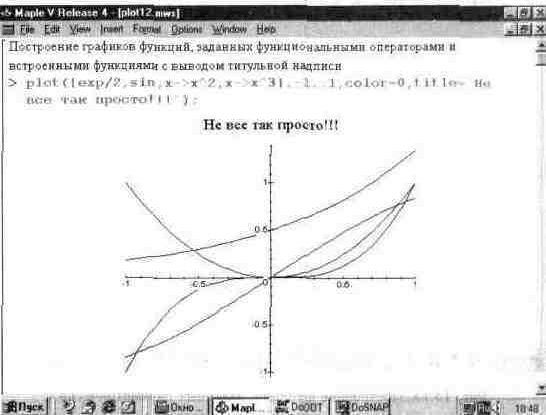
Рис. 13.12. Построение графиков функции, заданной функциональными операторами.

Имена функции (без указания списка параметров в круглых скобках тоже по существу являются функциональными операторами. Так что и они могут использоваться при построении графиков упрощенными способами.

13.2.11. Построение графиков функций, заданных параметрически

В ряде случаев для задания некоторых зависимостей используются заданные параметрически уравнения, например x=fl(t) и y=f2(t) при изменении переменной t в некоторых пределах. Точки (х,у) наносятся на график в Декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:

plot([fl(t),f2(t),t=tmin..tmax],h,v,p)

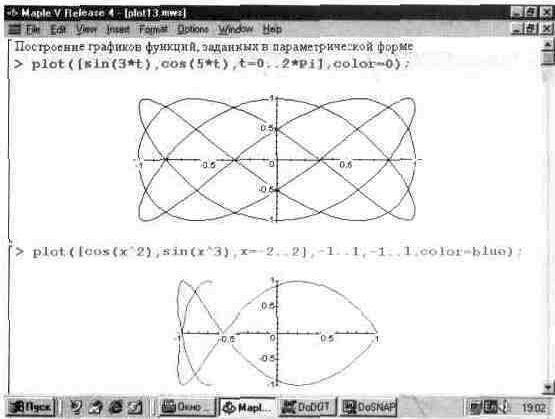
Если функции fl(t) и f2(t) содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t задается обычно 0..2*Pi или -Pi..Pi. К примеру, если задать в качестве функций fl(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рис. 13.!3 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.

Задание указателей масштаба h и v, а также параметров р не обязательно. Но, как и ранее, позволяет получить вид графика, удовлетворяющий всем требования пользователя.

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата