Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

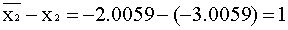
x1=b15-b14. x4-b13. x13-b12. x2=-0. 9731-0. 2043(-2. 2850)-0. 6559. 6. 4986-0. 2602.

(-3. 0059)=-3. 9866

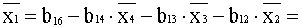1. 1473-0. 2043(-1. 2850)-0. 6559. 7. 4986-

-0. 2602. (-2. 0059)=-2. 9866

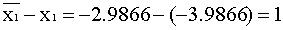
Вывод по решению:

В результате проделанной работы мы решили систему из четырёх уравнений методом Гаусса и получили: X1=-2. 2850; X2= 6. 4986; X3=-3. 0059; X4=-3. 9866.

4. Задача 4 4. 1. Постановка задачи

Дано дифференциальное уравнение :

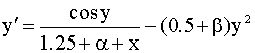
где a =0,5 b =0

Начальное условие y(0)=0

Необходимо найти методом Рунге-Кутта его решение на отрезке [ 0;0,3]

c шагом h=0. 1

4. 2. Решение

Дифференциальное уравнение :

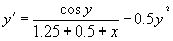
решаем методом Рунге-Кутта по вычислительной схеме приведенной в методическом указании по выполнению курсовой работы.

Для вычисления воспользуемся таблицей 4. 1. включив в неё вычисления правой части f(x,y).

Наиболее часто используется метод численного интегрирования дифференциальных уравнений первого порядка.

y'=f(x,y), y(x0)=y

Метод Рунге-Кутта четвёртого порядка.

В этом методе на одном шаге интегрирования при вычислении

yi+1=yi+D yi

приращение D yi определяется как сумма четырёх приращений взятых с различными весовыми коэффициентами :

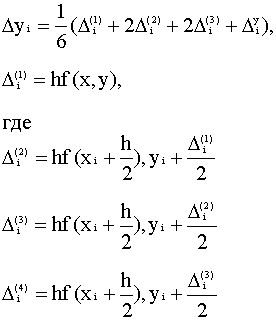
Рекомендуем скачать другие рефераты по теме: охрана труда реферат, шпоры по уголовному.

Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата