|
1.
|
[p] [q]

r
|
Доказательство в исчислении высказываний есть по существу
последовательность преобразований высказывания р с целью показать, что р
общезначимо. Каждый шаг в доказательстве есть либо уже доказанное высказывание, либо высказывание, истинное по предположению и вводимое для последующих шагов.
Каждый шаг , который является предположением, заключается в скобки [ ]. Все
другие шаги должны быть доказаны. Последним шагом в доказательстве должно быть
само высказывание р.
Докажем высказывание 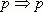
[p]
p
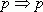 Правило
I
Правило
I
Первым шагом мы делаем предположение, что р - общезначима. Тогда второй шаг
непосредственно следует из первого. Раз мы предположили общезначимость р на
первом шаге, то мы используем этот факт на втором. На третьем шаге мы
используем правила вывода I, которое устанавливает общезначимость высказывания 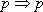 .
.
Доказательство с помощью правил вывода гибче, чем доказательство с помощью
таблицы истиности. В первом случае мы можем проанализировать каждый шаг в
цепочке доказательства. В то же время, неограниченный рост таблицы истиности не
позволят нам этого сделать.
Присмотревшись внимательно к правилам вывода, можно увидеть, что они хорошо
согласуются с нашей интуицией. Например, возьмём правило VIII. Если на предыдущих
шагах была доказана общезначимость высказываний p и q, то очевидно что высказывание 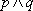 - тоже общезначимо.
- тоже общезначимо.
Итак, в дальнейшем при доказательстве мы будем использовать либо правила
эквивалентности (в этом случае каждый шаг будет замещением правого вхождения в
высказывании на левую часть правила) либо правила вывода.
5.2.4. Некоторые приёмы доказательства.
Дедуктивный вывод.
Доказать 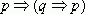
[p] - Предположение
[q] - Предположение
р - 1.
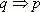 - I, 2, 3
- I, 2, 3
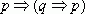 - I, 1, 4
- I, 1, 4
Мы предположили общезначимость утверждений p и q и воспользовавшись правилом I. введение  .
.
Использование правила Моdus Рonens. Это правило хорошо
работает когда надо доказать высказывания типа “Если в этом кинотеатре дают
“Анаконду”, то я куплю билеты.” Если кто-то сделал это утверждение и вы
увидели, что в кинотеатре идет “Анаконда”, то вы можете заключить, что этот
человек купил билеты.
Доказать 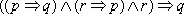
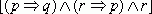 - Предположение
- Предположение
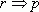 - IX. Удаление
- IX. Удаление  , 1
, 1
r
- IX. Удаление  , 1
, 1
р
- III. Моdus Рonens, 2, 3
p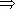 q
- IX. Удаление
q
- IX. Удаление
 , 1
, 1
q
- III. Моdus Рonens. 4, 5
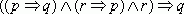 - I. Введение
- I. Введение 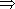 , 1, 6
, 1, 6
Использование Моdus Tollens.
Доказать 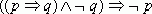
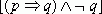 - Предположение
- Предположение
p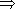 q - IX. Удаление
q - IX. Удаление  , 1
, 1
Øq
- IX. Удаление  , 1
, 1
Øp
- III.2. Modus Tollens, 2, 3
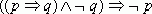 - I. Введение
- I. Введение 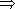 , 1, 4
, 1, 4
Использование Введения Ø и Удаления Ø .
Докажем 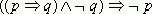
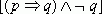 -
Предположение
-
Предположение
p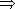 q - IX. Удаление
q - IX. Удаление  , 1
, 1
Øq
- IX. Удаление  , 1
, 1
[p] -
Предположение
q
- III. Моdus Ðonens, 4, 2
Øq - 3
F
- VI. Удаление  , 5, 6
, 5, 6
Øp
- V. Введение Ø 4, 7
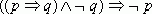 - I. Введение Ø 1, 8
- I. Введение Ø 1, 8
Рекомендуем скачать другие рефераты по теме: реферати, скачать дипломную работу.
Предыдущая страница реферата |
12
13
14
15
16
17
18
19
20
21
22 |
Следующая страница реферата
![]()
 Главная
Главная