Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

3-й шаг. Первой группе присваивается символ 0, второй группе символ 1.

4-й шаг. Каждую из образованных подгрупп делят на две части таким образом, чтобы суммарные вероятности вновь образованных подгрупп были по возможности равны.

5-й шаг. Первым группам каждой из подгрупп вновь присваивается 0, а вторым - 1. Таким образом, мы получаем вторые цифры кода. Затем каждая из четырех групп вновь делится на равные (с точки зрения суммарной вероятности) части до тех пор, пока в каждой из подгрупп не останется по одной букве.

Согласно методике Хаффмена, для построения оптимального кода N символы первичного алфавита выписываются в порядке убывания вероятностей. Последние  символов, где [6] и  - целое число, объединяют в некоторый новый символ с вероятностью, равной сумме вероятностей объединенных символов Последние символы с учетом образованного символа вновь объединяют, получают новый, вспомогательный символ, опять выписывают символы в порядке убывания вероятностей с учетом вспомогательного символа и т. д. до тех пор, пока сумма вероятностей т оставшихся символов после -го выписывания в порядке убывания вероятностей не даст в сумме вероятность, равную 1. На практике обычно, не производят многократного выписывания вероятностей символов с учетом вероятности вспомогательного символа, а обходятся элементарными геометрическими построениями, суть которых сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность. Затем с учетом вновь образованных символов, которым присваивается значение суммарной вероятности двух предыдущих, строят кодовое дерево, в вершине которого стоит символ с вероятностью 1. При этом отпадает необходимость в упорядочивании символов кодируемого алфавита в порядке убывания вероятностей.

Построенные по указанным выше (либо подобным) методикам коды с неравномерным распределением символов, имеющие минимальную среднюю длину кодового слова, называют оптимальным, неравномерным, кодами (ОНК). Равномерные коды могут быть оптимальными только для передачи сообщений с равновероятным распределением символов первичного алфавита, при этом число символов первичного алфавита должно быть равно целой степени числа, равного количеству качественных признаков вторичного алфавита, а в случае двоичных кодов - целой степени двух.

Максимально эффективными будут те ОНК, у которых

Для двоичных кодов

                                                (52)

так как log22 = 1. Очевидно, что равенство (52) удовлетворяется при условии, что длина кода во вторичном алфавите

Величина  точно равна Н, если , где п - любое целое число. Если п не является целым числом для всех значений букв первичного алфавита, то  и, согласно основной теореме кодирования[7], средняя длина кодового слова приближается к энтропии источника сообщений по мере укрупнения кодируемых блоков.

Эффективность ОНК. оценивают при помощи коэффициента статистического сжатия:

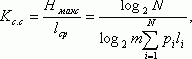                                             (53)

который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением методов нестатистического кодирования и коэффициента относительной эффективности

                                                                 (54)

который показывает, насколько используется статистическая избыточность передаваемого сообщения.

Для наиболее общего случая неравновероятных и взаимонезависимых символов

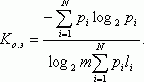
Для случая неравновероятных и взаимозависимых символов

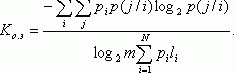
ТЕМА 6. ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК В СООБЩЕНИЯХ

Понятие об идее коррекции ошибок

Для того чтобы в принятом сообщении можно было обнаружить ошибку это сообщение должно обладать некоторой избыточной  информацией, позволяющей отличить ошибочный код от правильного Например, если переданное сообщение состоит из трех абсо­лютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следую­щим примером:

10110 - переданная кодовая комбинация;

10010 - 1-я принятая комбинация;

Рекомендуем скачать другие рефераты по теме: реферат федерация, сочинение капитанская.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата