ИССЛЕДОВАНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

1. Целью работы является:

- теоретическое изучение логических элементов, реализующих элементарные функции алгебры логики (ФАЛ);

- экспериментальное исследование логических элементов, построенных на отечественных микросхемах серии К155.

2. Основные теоретические положения.

2.1. Математической основой цифровой электроники и вычислительной техники является алгебра логики или булева алгебра (по имени английского математика Джона Буля).

В булевой алгебре независимые переменные или аргументы (X) принимают только два значения: 0 или 1. Зависимые переменные или функции (Y) также могут принимать только одно из двух значений: 0 или 1. Функция алгебры логики (ФАЛ) представляется в виде:

Y = F (X1; X2; X3 ... XN ).

Данная форма задания ФАЛ называется алгебраической.

2.2. Основными логическими функциями являются:

- логическое отрицание (инверсия)

- логическое сложение (дизьюнкция)

- логическое умножение (коньюнкция)

К более сложным функциям алгебры логики относятся:

- функция равнозначности (эквивалентности)

- функция неравнозначности (сложение по модулю два)

- функция Пирса (логическое сложение с отрицанием)

- функция Шеффера (логическое умножение с отрицанием)

2.3. Для булевой алгебры справедливы следующие законы и правила:

- распределительный закон

- правило повторения

- правило отрицания

- теорема де Моргана

- тождества

2.4. Схемы, реализующие логические функции, называются логическими элементами. Основные логические элементы имеют, как правило, один выход (Y) и несколько входов, число которых равно числу аргументов (X1;X2;X3 ... XN). На электрических схемах логические элементы обозначаются в виде прямоугольников с выводами для входных (слева) и выходных (справа) переменных. Внутри прямоугольника изображается символ, указывающий функциональное назначение элемента.

На рис.1 ё 10 представлены логические элементы, реализующие рассмотренные в п.2.2. функции. Там же представлены так называемые таблицы состояний или таблицы истинности, описывающие соответствующие логические функции в двоичном коде в виде состояний входных и выходных переменных. Таблица истинности является также табличным способом задания ФАЛ.

На рис.1 представлен элемент “НЕ”, реализующий функцию логического отрицания.

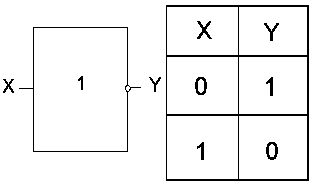
Рис. 1

Элемент “ИЛИ” (рис.2) и элемент “И” (рис.3) реализуют функции логического сложения и логического умножения соответственно.

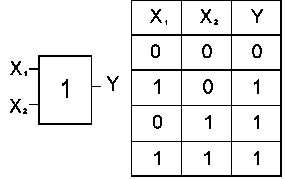
Рис. 2

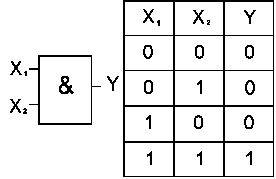
Рис. 3

Функции Пирса и функции Шеффера реализуются с помощью элементов “ИЛИ-НЕ” и “И-НЕ”, представленных на рис.4 и рис. 5 соответственно.

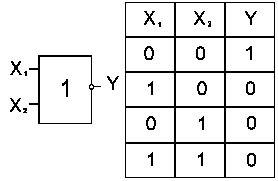
Рис. 4

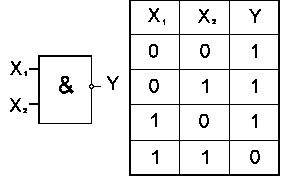
Рис. 5

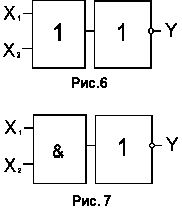
Элемент Пирса можно представить в виде последовательного соединения элемента “ИЛИ” и элемента “НЕ” (рис.6), а элемент Шеффера - в виде последовательного соединения элемента “И” и элемента “НЕ” (рис.7).

Рекомендуем скачать другие рефераты по теме: изложение с элементами сочинения, доклад по физкультуре.

1  2 | Следующая страница реферата