Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



Пусть имеем систему линейных уравнений:

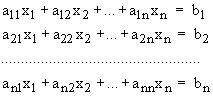
Простой метод Гаусса состоит в следующем.

Составим расширенную матрицу, приписав к матрице коэффициентов СЛУ дополнительный столбец – правые части уравнения:

.

Выполним над строками расширенной матрицы преобразования, аналогичные тем, которые были описаны в п. 2.1:

,

,

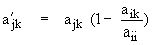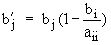и приведем ее к треугольному виду:

.

Теперь можно вычислить искомые величины xi , начиная с последнего, т.е. вначале находится xn , затем xn-1, xn-2, … , x1. Формула для вычислений имеет вид:

.

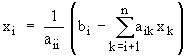Для расширения возможностей и повышения устойчивости приведенного алгоритма используется выбор главного элемента. Порядок метода Гаусса равен O(n3).

2.5. Метод обращения матрицы

Представим систему линейных уравнений в матричной форме:

.

Умножим последнее равенство слева на A-1 :

.

Учитывая, что A-1× A = I , формально получаем искомое решение:

Таким образом, решение системы выполняется в два этапа:

1) вычисление обратной матрицы;

2) умножение обратной матрицы на вектор правых частей СЛУ.

Несмотря на то, что метод обращения матрицы имеет такой же порядок, как и метод Гаусса - O(n3), по объему вычислений он проигрывает ему в несколько раз. Однако, если СЛУ необходимо решать многократно и при этом изменяется лишь вектор правых частей, метод обращения матрицы становится все же выгодным.

Практическая часть

Описание класса Matrix для решения задач линейной алгебры

Класс имеет приватные и общедоступные члены-данные и члены-функции (методы). Для хранения компонентов матрицы используется одномерный динамический массив элементов типа параметра шаблона. Для создания объекта предусмотрены три конструктора: конструктор по умолчанию, конструктор с параметрами, конструктор копирования и деструктор. Для выполнения множества матричных операций созданы перегруженные операции: присваивания (=), сложения (+), вычитания (-), умножения(*) и т.п. На базе операторов ввода/вывода С++ разработаны функции ввода матриц из потока и вывода их в поток, предусматривающие в случае файлового ввода/вывода как текстовую форму хранения, так и бинарную.

Доступ к членам-данным класса – числу строк и столбцов матрицы осуществляется с помощью методов size_row( ) и size_col( ). Для доступа к элементам матрицы создан перегруженный оператор вызова функции operator( ) (dim x, dim x), где dim – переопределенный тип unsigned char. Вызов функции используется как оператор индексирования, принимающий два аргумента. Аналогично создан оператор вызова функции с одним аргументом operator( ) (dim x). Для данного класса – это очень важные перегруженные операторы, т.к. они используются во всех функциях и операторах, в которых происходит обращение к элементам матрицы.

Описание функций, конструкторов и деструкторов класса:

Конструктор по умолчанию Matrix( ):

Конструктор по умолчанию создает матрицу нулевого размера. В дальнейшем размер этой матрицы можно изменить с помощью функции newsize(i, j).

Конструктор с параметрами Matrix(dim, dim=1):

Это обычный конструктор с параметрами, который принимает в качестве параметров размеры матрицы и создает одномерный динамический массив размером m*n, где m – число строк, а n – число столбцов матрицы. С целью возможности использовать его для создания векторов, второй параметр конструктора задан как умалчиваемый со значением 1. Для первоначальной “инициализации” элементов матрицы нулями используется функция setmem( ).

Конструктор копирования Matrix(const Matrix &):

Конструктор принимает в качестве параметра ссылку на объект класса (на существующую матрицу), определяет ее размер, выделяет для нее память и копирует в эту память содержимое матрицы, принимаемой по ссылке. Таким образом, создается точная копия матрицы с текущими значениями ее элементов.

Деструктор ~Matrix( ):

Деструктор высвобождает память, выделенную конструкторами для элементов матрицы.

Функция операции присваивания "=" Matrix& operator= (Matrix&):

Данная функция сравнивает адрес передаваемого по ссылке объекта с адресом собственного класса, чтобы не предпринялась попытка присвоит объект самому себе. После этого создается новый массив с числом элементов, равным числу элементов массива принимаемого по ссылке, и в этот массив заносится содержимое принимаемого массива. Возвращается разыменованный указатель this (return *this;).

Функции операций суммирования, вычитания, умножения матриц и умножения матрицы на число:

Эти функции реализованы как дружественные функции и алгоритмы этих функций аналогичны по своему составу. Общий вид прототипа этих функций: friend Matrix operator @(const Matrix&, const Matrix&). Применение дружественных функций в данном случае целесообразно для того, чтобы иметь возможность передавать в оператор функцию объекты в любой последовательности. В этих операторах-функциях вначале создается временный объект типа матрица (с помощью конструктора копирования), в который копируется первая матрица и который при выходе из функции является возвращаемым объектом. Затем эта матрица суммируется (вычитается, умножается) с матрицей, стоящей после знака оператора по соответствующим правилам матричных операций. При этом для доступа к элементам матрицы и индексирования используются перегруженные операторы вызова функции operator( ) (dim x, dim x) и operator( ) (dim x).

Функция – оператор Matrix operator^ (int):

Этот оператор-функция реализован как член класса и предназначен для возведения матрицы в степень. В случае, когда значение входного параметра равно минус единице осуществляется вызов функции вычисления обратной матрицы методом преобразований Гаусса, для чего разработана отдельная функция Matrix & Gauss(dim, dim). Таким образом, использование этого оператора позволяет решать систему линейных алгебраических уравнений в представлении X = (A^-1)*B, где X и B –вектора неизвестных и правых частей соответственно.

Функция – оператор Matrix operator ! ( ):

Оператор для определения транспонированной матрицы.

Рекомендуем скачать другие рефераты по теме: инновационная деятельность, решебник по английскому языку.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата