Усложнение решающего правила при управлении в задачах распознавания образов

Бекмуратов К.А.

Рассматривается один из возможных принципов усложнения решающего правила непрерывного пространства признаков, порождаемого опорными объектами конкретного образа. Предложена процедура нахождения предельного значения размерности признакового пространства, в котором возможно кусочно-линейное разделение образов и гарантированы требуемые качество и надежность распознавания, необходимые в системах управления.

В работе [1] описан метод формирования пространства непрерывных признаков, приводящий к безошибочному разделению образов. Введено понятие непрерывного признака и показано, что если набирать пространство только из определенных в [1] признаков, то можно достичь безошибочного разделения  образов.

В данной работе так же, как и в [2], рассмотрим случай, когда в пространстве непрерывных признаков размерности n безошибочное разделение обучающей последовательности невозможно.

Пусть на некотором множестве  мощности  объектов  определены подмножества  при , представляющие собой образы на обучающей выборке    

Допустим, что  - подмножество на  , соответствующее конкретному образу , а  - подмножество на  , соответствующее остальным   образом

Требуется с использованием обучающую выборки  найти решающее правило , указывающее принадлежность  любого объекта из  одному   

из заданных образов  или  с вероятностью ошибки,  не превышающей ,  достигаемой с надежностью (1-), и определить целесообразности усложнения решающих правил при синтезе непрерывных признаковых пространств.

Если обучающая последовательность не может быть безошибочно разделима выбранным решающим правилом, то в общем случае справедлива теорема Вапника - Червоненкиса [3], смысл которой состоит в том, что если в n-мерном пространстве признаков решающее правило совершает  ошибок при классификации обучающей последовательности длины   , то с вероятностью можно утверждать, что вероятность ошибочной классификации составит величину, меньшую ,

,

где N- число всевозможных правил заданного класса, которое можно построить в пространстве заданной размерности.

Предположим, что в процессе обучения из последовательно поступивших непрерывных свойств относительно  опорных объектов  синтезирована подсистема непрерывных признаков. В зависимости от состава случайной и независимой выборки процесс обучения может остановиться при любом значении n, но если разделение конкретной обучающей выборки наступило в n-мерном пространстве, то число N всевозможных решающих правил в классе не должно превышать числа всех подмножеств множества, состоящего из элементов, т.е.

,                                                      

где                                                   

.

Логарифмируя получим

                                       (1)

Если учесть    , то  (1) принимает вид

,                                 (2)

где  можно оценить в виде

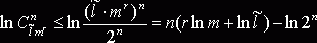                                       (3)

Подставляя (3) в (2), получаем

                                                   (4)

Используя теорему Вапника-Червоненкиса [3], можно вычислить предельную размерность пространства

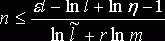,                                                    (5)

Рекомендуем скачать другие рефераты по теме: сочинение по картине, рефераты на казахском.





1  2 | Следующая страница реферата