Аппроксимация функций
| Категория реферата: Рефераты по математике
| Теги реферата: конспект по русскому, бесплатные решебники скачать
| Добавил(а) на сайт: Kuzarin.
Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата
S=-1.594203
АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.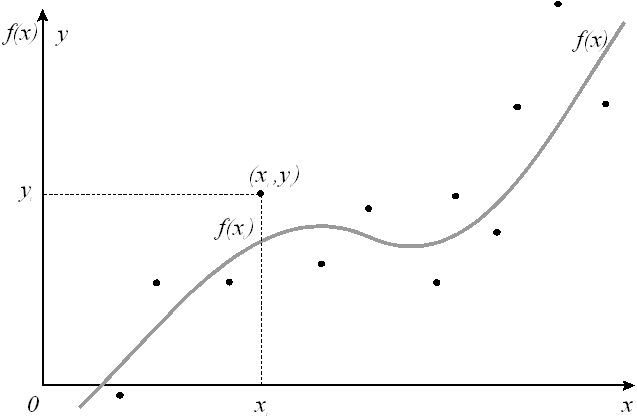
В инженерной деятельности часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек с координатами (xi,yi), i=0,1,2,...n, где n - общее количество точек. Как правило, эти табличные данные получены экспериментально и имеют погрешности. При аппроксимации желательно получить относительно простую функциональную зависимость (например, полином), которая позволила бы "сгладить" экспериментальные погрешности, получить промежуточные и экстраполяционные значения функций, изначально не содержащиеся в исходной табличной информации.
Графическая интерпретация аппроксимации.Эта функциональная (аналитическая) зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. Критерием точности или достаточно "хорошего" приближения могут служить несколько условий.
Обозначим через fi значение, вычисленное из функциональной зависимости для x=xi и сопоставляемое с yi.
Одно из условий согласования можно записать как
S =
(fi-yi)
min ,
т.е. сумма отклонений табличных и функциональных значений для одинаковых x=xi должна быть минимальной (метод средних). Отклонения могут иметь разные знаки, поэтому достаточная точность в ряде случаев не достигается.
Использование критерия S = |fi-yi| min , также не приемлемо, т.к. абсолютное значение не имеет производной в точке минимума.
Учитывая вышеизложенное, используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость, при которой S = (fi-yi)2 , (1)
обращается в минимум.
В качестве функциональной зависимости рассмотрим многочлен
f(x)=C0 + C1X + C2X2+...+CMXM. (2)Формула (1) примет вид S = 
(
C0 + C1Xi + C2Xi2+...+CMXiM
- Yi ) 2
Условия минимума S можно записать, приравнивая нулю частные производные S по независимым переменным С0,С1,...СМ :
SC0 = 2 ( C0 + C1Xi
+ C2Xi2+...+CMXiM
- Yi ) = 0 , SC1 = 2 ( C0 + C1Xi
+ C2Xi2+...+CMXiM
- yi ) Xi = 0 ,(3)
SCM = 2 ( C0 + C1Xi
+ C2Xi2+...+CMXiM
- Yi ) XiM = 0 , Тогда из (3) можно получить систему нормальных уравнений
C0(N+1) + C1
Xi + C2Xi2
+...+ CMXiM
= Yi , C0Xi +
C1Xi2
+ C2Xi3
+...+ CMXiM+1
= Yi Xi ,(4)
C0XiM
+ C1XiM+1
+ C2XiM+2
+...+ CMXi2M
=Yi XiM
.
Для определения коэффициентов Сi и, следовательно, искомой зависимости (2) необходимо вычислить суммы и решить систему уравнений (4). Матрица системы (4) называется матрицей Грама и является симметричной и положительно определенной. Эти полезные свойства используются при ее решении.
|
(N+1) |
|
|
... |
|
|
|
Xi |
|
|
... |
|
|
|
... |
... |
... |
... |
... |
... |
|
XiM |
|
|
Категории:Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
Главная