«Безвихревая электродинамика». Математическая модель

Кузнецов Ю.Н.

Уравнение симметрийно-физического перехода в электромагнитных явлениях.

В математических моделях природных явлений реальным геометрическим симметриям описываемых объектов соответствуют геометрические симметрии тензорных величин. Чем ниже ранг тензора, тем выше степень его предельной геометрической симметрии.

Отобразим симметрийно-физический переход в локальной электродинамике посредством рангового преобразования. С этой целью умножим на безразмерный

4-вектор известное максвелловское уравнение

‡‡. (1)

В результате двумя уравнениями с тензорами первого и нулевого рангов описываются разные симметрии физически наполненных геометрических величин.

Соответственно, разные свойства у двух видов источников и их полей, разные причинно-следственные связи у одной и той же природной сущности.

Сведём к нулю в правом уравнении производную по времени. В итоге получаем дифференциальную форму записи известной электростатической теоремы Гаусса

ÑÑ. (2)

И новое гауссоподобное дифференциальное уравнение для более симметричной локальной магнитостатики с потенциальным магнитным полем, образуемым безнаправленными (в общем случае – бесконечно малыми сферическими) центрально-симметричными токами зарядов

Ñ Ñ  . (3)

Приравнивая нулю источники поля в левом и правом уравнениях равенства (1), получаем математическое описание симметрийно-физического перехода для ЭМВ в пустом пространстве. Перехода поперечных ЭМВ в продольные.

В общем случае ранговое преобразование описывает ступенчатый переход к другой геометрической симметрии тензорных величин, сопровождаемое ступенчатым

изменением их физического наполнения.

В случае практической реализации симметрийно-физического перехода в каком-либо конкретном явлении ранговое преобразование представляет собой его теоретическую модель.

Оно может использоваться в предсказательных целях, являясь разновидностью метода математической гипотезы.

Построение математической модели безвихревой электродинамики. В результате анализа центрально-симметричной магнитостатики [1] была получена формула, связывающая потенциал и напряжённость стационарного магнитного поля

 (4)

Переходя к описанию переменного поля, посредством умножения обеих частей

равенства (4) на оператор , имеем формулу

, (5)

отображающую локальное явление электромагнитной индукции вне вещественного источника.

Используя принцип перестановочной двойственности [2], трансформируем формулу (5) в запись явления магнитоэлектрической индукции

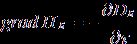. (6)

Рекомендуем скачать другие рефераты по теме: взаимодействие реферат, большие рефераты.





1  2  3  4  5  6  7 | Следующая страница реферата