|
0,376292 |
-0,08927 |
-0,28847 |
-0,21319 |
-0,00664 |
0,149756 |
0,156231 |
0,041675 |
2,347436 |
|
1499 |
0,974174 |
0,816945 |
0,548165 |
0,24339 |
-0,01759 |
-0,1767 |
-0,21446 |
-0,15215 |
-0,03951 |
0,066542 |
2,048811 |
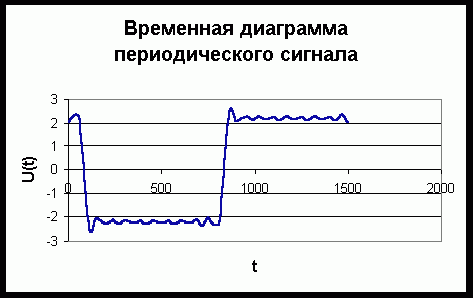
После расчета строим временную диаграмму
сигнала
2.2.ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТОВ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
Для того чтобы определить амплитудно-частотную и фазочастотную характеристику периодического сигнала представим сигнал в виде ряда Фурье (2). Коэффициенты ряда Аn и Bn определяются по формулам (1) . Для того чтобы вычислить An и Bn преобразуем интеграл к сумме, а непрерывную функцию U(t) представим как дискретную (t1) , где tI=i*TД (ТД – интервал дискретизации).
Представим непрерывную функцию U(t) как дискретную, сделав замену t i * ТД
и di ТД, преобразуем выражения An ,Bn
и запишем ряд Фурье в окончательном виде:
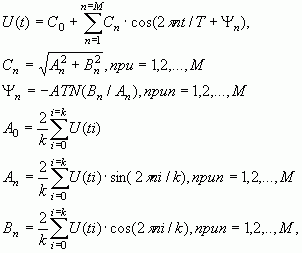 ( 5)
( 5)
где k=T/ТД – число отсчётов сигнала на интервале T. Интервал дискретизации ТД выбираем таким, чтобы на самом крутом участке функции U(t) , было не менее 5 отсчётов, либо не менее 5 отсчётов на периоде наибольшей частоты в спектре сигнала. Исходя из формулы(5),вычисляем амплитудно-частотную и фазочастотную характеристики. Расчеты приведены в таблице


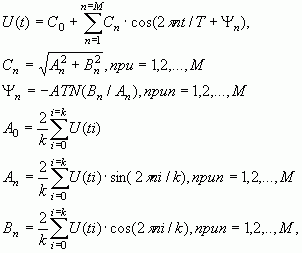 ( 5)
( 5) Главная
Главная