Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Докажем эту формулу также методом математической индукции.

а) При n=1 получим b1=b1*q^0=b1. Следовательно, формула верна.

б) Пусть k - любое натуральное число и пусть формула справедлива при n=k, то есть

bk= b1*q^(k-1).

По определению геометрической прогрессии имеем bk+1=bk*q. Подставим в это равенство выражение для bk, которое, согласно предположению индукции, считаем верным. Получим

bk+1= b1*q^(k-1)*q= b1*qk.

Значит формула (3) верна для всех n.

Основное свойство геометрической прогрессии.

Последовательность не равных нулю чисел b1, b2, b3, ..., bn, ... является геометрической прогрессией тогда и только тогда, когда квадрат каждого её члена, начиная со второго, равен произведению двух соседних с ним членов, то есть

bn^2=bn-1*bn+1, n³ 2.

Формулы суммы n первых членов геометрической прогрессии:

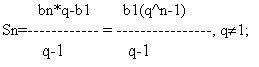(4)

Sn=b1*n, q=1.

Задача 2. Согласно древней легенде индийский царь Шерам был восхищен новой игрой - шахматами и предложил её изобретателю - мудрецу Сете любую награду. Сете попросил плату пшеницей исходя из следующего расчёта: за первую клетку доски заплатить 1 зерно, за вторую 2 зерна, за третью 4 зерна, и т.д. - за каждую следующую клетку дать в 2 раза больше зёрен, чем за предыдущую. Сколько зёрен потребовал Сете за изобретение шахмат?

Решение. Последовательность чисел, которая показывает, сколько зёрен должен был заплатить царь за каждую из 64 клеток шахматной доски, является геометрической прогрессией с первым членом b1=1 и знаменателем q=2. Чтобы найти количество зёрен, нам надо найти сумму

S64=1+2+2^2+2^3+...+2^63.

Воспользуемся формулой (4) и получим

Это очень большое число. Если его посчитать, то получится 18446744073709551615 (восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать !) К сожалению, при вычислении такого числа нельзя воспользоваться ни микрокалькулятором, ни персональным компьютером, так как это число содержит 20 цифр, а МК, например, даёт только восемь первых точных цифр, ПК - шестнадцать.

3. Бесконечно убывающей геометрической прогрессией называют геометрическую прогрессию, у которой модуль знаменателя меньше единицы, то есть q<1.

Сумма всех членов бесконечно убывающей геометрической прогрессии вычисляется по формуле

Проценты.

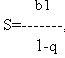
Процентом (от лат. “pro cento” - с сотни) числа называется сотая часть этого числа.

Три основные задачи на проценты таковы:

Задача 1. Найти указанный процент данного числа.

Для этого данное число умножается на число процентов; результат делится на 100, то есть

Рекомендуем скачать другие рефераты по теме: рефераты по истории россии, титульный лист курсовой работы.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата