
Дисперсионный анализ
| Категория реферата: Рефераты по математике
| Теги реферата: реферат отрасль, реферат электрические
| Добавил(а) на сайт: Роман.
Предыдущая страница реферата | 15 16 17 18 19 20 21 22 23 24 25 | Следующая страница реферата
Оценить
параметры приведенной формы VAR легко. Каждое из уравнений содержит одни и те
же регрессоры (Yt–1,...,Yt–p), и нет взаимных ограничений между уравнениями.
Таким образом, эффективная оценка (метод максимального правдоподобия с полной
информацией) упрощается до обычного МНК, примененного к каждому из уравнений.
Матрицу ковариаций ошибок ![]() можно состоятельно
оценить выборочной ковариационной матрицей полученных из МНК остатков.
можно состоятельно
оценить выборочной ковариационной матрицей полученных из МНК остатков.
Единственная тонкость – определить длину лага p, но это можно сделать, используя информационный критерий, такой как AIC или BIC.
На уровне матричных уравнений рекурсивная и структурная VAR выглядят одинаково. Эти две модели VAR учитывают в явном виде одновременные взаимодействия между элементами Yt, что сводится к добавлению одновременного члена к правой части уравнения (17). Соответственно, рекурсивная и структурная VAR обе представляются в следующем общем виде:
![]() (18)
(18)
где - вектор констант;
B0,..., Bp - матрицы;
t — ошибки.
Наличие в уравнении матрицы B0 означает возможность одновременного взаимодействия между n переменными; то есть B0 позволяет сделать так, чтобы эти переменные, относящиеся к одному моменту времени, определялись совместно.
Рекурсивную VAR можно оценить двумя способами. Рекурсивная структура дает набор рекурсивных уравнений, которые можно оценить с помощью МНК. Эквивалентный способ оценивания заключается в том, что уравнения приведенной формы (17), рассматриваемые как система, умножаются слева на нижнюю треугольную матрицу.
Метод оценивания структурной VAR зависит от того, как именно идентифицирована B0. Подход с частичной информацией влечет использование методов оценивания для отдельного уравнения, таких как двухшаговый метод наименьших квадратов. Подход с полной информацией влечет использование методов оценивания для нескольких уравнений, таких как трехшаговый метод наименьших квадратов.
Необходимо помнить о множественности различных типов VAR. Приведенная форма VAR единственна. Данному порядку переменных в Yt соответствует единственная рекурсивная VAR, но всего имеется n! таких порядков, т.е. n! различных рекурсивных VAR. Количество структурных VAR – то есть наборов предположений, которые идентифицируют одновременные взаимосвязи между переменными, - ограничено только изобретательностью исследователя.
Поскольку матрицы оцененных коэффициентов VAR затруднительно интерпретировать непосредственно, результаты оценивания VAR обычно представляют некоторыми функциями этих матриц. К таким статистикам разложения ошибки прогноза.
Разложения дисперсии ошибки прогноза вычисляются в основном для рекурсивных или структурных систем. Такое разложение дисперсии показывает, насколько ошибка в j-м уравнении важна для объяснения неожиданных изменений i-й переменной. Когда ошибки VAR некоррелированы по уравнениям, дисперсию ошибки прогноза на h периодов вперед можно записать как сумму компонентов, являющихся результатом каждой из этих ошибок /17/.
3.2 Факторный анализ
В современной статистике под факторным анализом понимают совокупность методов, которые на основе реально существующих связей признаков (или объектов) позволяют выявлять латентные обобщающие характеристики организационной структуры и механизма развития изучаемых явлений и процессов.
Понятие латентности в определении ключевое. Оно означает неявность характеристик, раскрываемых при помощи методов факторного анализа. Вначале имеется дело с набором элементарных признаков Xj, их взаимодействие предполагает наличие определенных причин, особенных условий, т.е. существование некоторых скрытых факторов. Последние устанавливаются в результате обобщения элементарных признаков и выступают как интегрированные характеристики, или признаки, но более высокого уровня. Естественно, что коррелировать могут не только тривиальные признаки Xj, но и сами наблюдаемые объекты Ni поэтому поиск латентных факторов теоретически возможен как по признаковым, так и по объектным данным.
Если объекты характеризуются достаточно большим числом элементарных признаков (m > 3), то логично и другое предположение - о существовании плотных скоплений точек (признаков) в пространстве n объектов. При этом новые оси обобщают уже не признаки Xj, а объекты ni, соответственно и латентные факторы Fr будут распознаны по составу наблюдаемых объектов:
Fr = c1n1 + c2n2 + ... + cNnN,
где ci - вес объекта ni в факторе Fr.
В зависимости от того, какой из рассмотренных выше тип корреляционной связи - элементарных признаков или наблюдаемых объектов - исследуется в факторном анализе, различают R и Q - технические приемы обработки данных.
Название R-техники носит объемный анализ данных по m признакам, в результате него получают r линейных комбинаций (групп) признаков: Fr=f(Xj), (r=1..m). Анализ по данным о близости (связи) n наблюдаемых объектов называется Q-техникой и позволяет определять r линейных комбинаций (групп) объектов: F=f(ni), (i = l .. N).
В настоящее время на практике более 90% задач решается при помощи R-техники.
Набор методов факторного анализа в настоящее время достаточно велик, насчитывает десятки различных подходов и приемов обработки данных. Чтобы в исследованиях ориентироваться на правильный выбор методов, необходимо представлять их особенности. Разделим все методы факторного анализа на несколько классификационных групп:
- Метод главных компонент. Строго говоря, его не относят к факторному анализу, хотя он имеет с ним много общего. Специфическим является, во-первых, то, что в ходе вычислительных процедур одновременно получают все главные компоненты и их число первоначально равно числу элементарных признаков. Во-вторых, постулируется возможность полного разложения дисперсии элементарных признаков, другими словами, ее полное объяснение через латентные факторы (обобщенные признаки).
- Методы факторного анализа. Дисперсия элементарных признаков здесь объясняется не в полном объеме, признается, что часть дисперсии остается нераспознанной как характерность. Факторы обычно выделяются последовательно: первый, объясняющий наибольшую долю вариации элементарных признаков, затем второй, объясняющий меньшую, вторую после первого латентного фактора часть дисперсии, третий и т.д. Процесс выделения факторов может быть прерван на любом шаге, если принято решение о достаточности доли объясненной дисперсии элементарных признаков или с учетом интерпретируемости латентных факторов.
Методы факторного анализа целесообразно разделить дополнительно на два класса: упрощенные и современные аппроксимирующие методы. Простые методы факторного анализа в основном связаны с начальными теоретическими разработками. Они имеют ограниченные возможности в выделении латентных факторов и аппроксимации факторных решений. К ним относятся:
- однофакторная модель. Она позволяет выделить только один генеральный латентный и один характерный факторы. Для возможно существующих других латентных факторов делается предположение об их незначимости;
- бифакторная модель. Допускает влияние на вариацию элементарных признаков не одного, а нескольких латентных факторов (обычно двух) и одного характерного фактора;
- центроидный метод. В нем корреляции между переменными рассматриваются как пучок векторов, а латентный фактор геометрически представляется как уравновешивающий вектор, проходящий через центр этого пучка. : Метод позволяет выделять несколько латентных и характерные факторы, впервые появляется возможность соотносить факторное решение с исходными данными, т.е. в простейшем виде решать задачу аппроксимации.
Современные аппроксимирующие методы часто предполагают, что первое, приближенное решение уже найдено каким либо из способов, последующими шагами это решение оптимизируется. Методы отличаются сложностью вычислений. К этим методам относятся:
- групповой метод. Решение базируется на предварительно отобранных каким-либо образом группах элементарных признаков;
- метод главных факторов. Наиболее близок методу главных компонент, отличие заключается в предположении о существовании характерностей;
- метод максимального правдоподобия, минимальных остатков, а-факторного анализа канонического факторного анализа, все оптимизирующие.
Эти методы позволяют последовательно улучшить предварительно найденные решения на основе использования статистических приемов оценивания случайной величины или статистических критериев, предполагают большой объем трудоемких вычислений. Наиболее перспективным и удобным для работы в этой группе признается метод максимального правдоподобия.
Основной задачей, которую решают разнообразными методами факторного анализа, включая и метод главных компонент, является сжатие информации, переход от множества значений по m элементарным признакам с объемом информации n х m к ограниченному множеству элементов матрицы факторного отображения (m х r) или матрицы значений латентных факторов для каждого наблюдаемого объекта размерностью n х r, причем обычно r < m. Методы факторного анализа позволяют также визуализировать структуру изучаемых явлений и процессов, а это значит определять их состояние и прогнозировать развитие. Наконец, данные факторного анализа дают основания для идентификации объекта, т.е. решения задачи распознавания образа. Методы факторного анализа обладают свойствами, весьма привлекательными для их использования в составе других статистических методов, наиболее часто в корреляционно-регрессионном анализе, кластерном анализе, многомерном шкалировании и др. /18/.
3.3 Парная регрессия. Вероятностная природа регрессионных моделей.
Если рассмотреть задачу анализа расходов на питание в группах с одинаковыми доходами, например в $10.000(x), то это детерминированная величина. А вот Y - доля этих денег, затрачиваемая на питание - случайна и может меняться от года к году. Поэтому для каждого i-го индивида:
![]()
где εi - случайная ошибка;
α и β - константы (теоретически), хотя могут меняться от модели к модели.
Предпосылки для парной регрессии:
- X и Y связаны линейно;
- Х - неслучайная переменная с фиксированными значениями;
- ε - ошибки нормально распределены N(0,σ2);
-
![]() ;
;
-
![]() .
.
На рисунке 3.1 представлена модель парной регрессии.
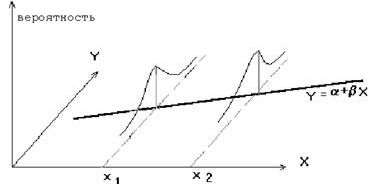
Рисунок 3.1 – Модель парной регрессии
Эти предпосылки описывают классическую линейную регрессионную модель.
Рекомендуем скачать другие рефераты по теме: лечение шпоры, шпаргалки по экономическому.
Категории:
Предыдущая страница реферата | 15 16 17 18 19 20 21 22 23 24 25 | Следующая страница реферата
 Главная
Главная