Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Однако обратим внимание на то, что циркуляционные векторы  и  в электродинамике Максвелла ([11] п. 12 и 14) имеют размерность линейной плотности физической величины, а потоковые векторы ,  и  – ее поверхностной плотности. В частности, размерность вектора магнитной индукции  равна поверхностной плотности момента импульса на единицу заряда, в системе СИ - Тесла. Экспериментально это ярко и наглядно иллюстрируется эффектом Эйнштейна-де Гааза, когда в среде при ее однородном намагничивании возникает коллинеарный вектору  механический вращающий момент, обусловленный упорядочением собственных моментов количества движения (спинов) электронов в атомах вещества среды. Поэтому, согласно соотношению (3а), вихревое поле магнитного вектор-потенциала  однозначно имеет размерность линейной плотности момента импульса на единицу заряда.

Как видим, магнитному потоку , то есть по физически оправданной аналогии с (10) “магнитному заряду” , сопоставляется его полевой эквивалент – поле магнитного векторного потенциала . В итоге имеем вторую фундаментальную корпускулярно-полевую пару , измеряемую в системе СИ (Джоуль∙секунда)/Кулон(Джоуль∙секунда)/(Кулон∙метр).

Соответственно, из соотношения (3c) размерность вихревого поля электрической напряженности  равна линейной плотности момента силы на единицу заряда, что никак не опровергает известное, а лишь вскрывает физический смысл этой физической величины, единица измерения которой в системе СИ – это Вольт/метр. Следовательно, соотношение (3c) есть полевой аналог уравнения динамики вращательного движения твердого тела в механике, что адекватно рассмотренным корпускулярно-полевым представлениям.

Итак, анализ исходных соотношений (3) позволил прояснить физический смысл ЭМ векторного потенциала как полевого эквивалента локальных основных параметров микрочастицы: заряда q и спина s. Таким образом, электрический заряд , кратный заряду электрона  создает электрическое поле с компонентами напряженности  и вектор-потенциала , а “магнитный заряд” – удельный (на единицу заряда) кинетический момент , кратный кванту магнитного потока  – магнитное поле с компонентами напряженности  и вектор-потенциала . Например, для электрона имеем из (10) и (11) конкретные выражения для компонент поля ЭМ векторного потенциала:  и . При этом микрочастица (совокупно, и макрообъект) обладает чисто электрической и магнитной энергиями, ЭМ энергией и моментом ЭМ импульса, условия реализации которых описываются соотношениями (7), (8), (2) и (9), соответственно.

Электродинамические аспекты теории нетеплового действия электрического тока в металлах.

В настоящее время установлено [13], что, как это ни парадоксально, металлы - это уникальная среда для изучения электродинамики нетепловых процессов. Лидером таких исследований является Троицкий [2-4], результаты работ которого, в частности, по ЭПЭ, как и его последователей у нас и за рубежом, нашли практическое применение в разнообразных технологиях обработки металлических материалов. Ниже на основе анализа следствий из представленных выше систем полевых уравнений обсуждаются электродинамические аспекты нетеплового действия постоянного электрического тока в металлах.

Начнем с традиционных уравнений ЭМ поля (1) для однородной проводящей среды в асимптотике металлов (). В стационарном приближении система указанных уравнений будет иметь вид:

(a) rot, (b) div, (c) rot, (d) div. (12)

Видно, что электрическая компонента ЭМ поля в проводнике при электропроводности потенциальна (12a), в объеме проводник локально электронейтрален (12b), а наличие тока порождает вихревую магнитную компоненту поля (12c).

Однако энергетически уравнения Максвелла способны описать лишь диссипативную составляющую физически сложного процесса электрической проводимости среды с помощью закона сохранения ЭМ энергии:

- div. (13)

Важно отметить, что перенос в пространстве потока ЭМ энергии принципиально реализуется посредством обеих компонент ЭМ поля в виде потокового вектора Пойнтинга . Этот поток, поступая извне в данную точку проводника (левая часть соотношения (13)), обеспечивает в нем электрический ток, что сопровождается выделением тепла, определяемого законом Джоуля-Ленца (правая часть (13)). Наиболее последовательно данный вопрос исследован (вплоть до построения картины “силовых” линий вектора Пойнтинга у поверхности проводника с током) в пособии по электродинамике Зоммерфельда [14].

Несмотря на наличие в проводнике с током электрической  и магнитной  компонент ЭМ поля, соответственно, электрической и магнитной энергий, из уравнений системы (12) не следуют для них соотношения баланса, аналогичные соотношению (13). Согласно уравнениям (12), такие энергетические потоки в принципе невозможны ввиду отсутствия в них вторых компонент электрического или магнитного полей. Поэтому в развитие представлений о взаимодействии металлов с ЭМ полем вместо стандартного описания электрического поля с помощью скалярного потенциала - grad , введем понятие поля электрического вектор-потенциала  проводника с током посредством соотношения rot. Такая альтернатива возможна, поскольку при электропроводности однородная проводящая среда остается по существу локально электронейтральной [15], а потому при ее электрической поляризации под действием тока div.

Здесь имеется полная математическая аналогия с полем магнитного векторного потенциала , когда из div следует представление вектора магнитной индукции в виде rot. Обсуждению свойств поля вектора  посвящена работа [12]. Отметим только, что если магнитный вектор-потенциал  считается вполне наблюдаемой физической величиной (эффекты Ааронова-Бома, Джозефсона, Мейснера и др.), то электрический вектор-потенциал  до настоящего времени как физическая реальность не рассматривался, а ему отводилась лишь роль формальной математической функции.

В применении к проводнику с током соотношение rot представим в интегральной форме:

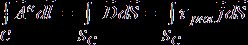, (14)

где циркуляция поля вектора электрического потенциала  по замкнутому контуру С равна потоку поля вектора электрического смещения  через поверхность SC , опирающуюся на этот контур. Согласно закону сохранения электрического заряда, этот поток через замкнутую поверхность () для постоянного тока равен нулю.

На основе (14) можно получить конкретные формулы связи поля вектора  с полями векторов  и , однородно распределенными внутри цилиндрического проводника радиуса R и ориентированными вдоль его оси симметрии:

 при r < R, (15)

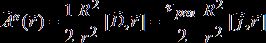 при r >R.

Таким образом, поле электрического вектор-потенциала  существует как в самом проводнике с током, так и вовне, оно непрерывно на его поверхности, при этом вектор  всегда ортогонален плоскости, в которой лежат вектора  и . Здесь интересно и физически перспективно представлять себе проводник с током в виде “электрического соленоида”, поскольку структуры полей электрической индукции  и вектор-потенциала  топологически тождественны аналогичным структурам полей магнитной индукции  и вектор-потенциала  магнитного соленоида [12].

Однако представления о вектор-потенциале  будут физически содержательны по-настоящему только тогда, когда указан, хотя бы в принципе, метод его наблюдения, а лучше - конкретный способ измерения параметров этого векторного поля. В рассматриваемом случае это возможно ввиду математической тождественности соотношений rot и rot, связанных выражением . А потому в асимптотике частот  “силовые” линии поля электрического вектор-потенциала  проводника с током топологически полностью соответствуют распределению напряженности магнитного поля , созданного этим током в процессе электропроводности, а величины этих полей во всех точках пространства прямо пропорциональны между собой:

.

Согласно [14], порядок величины постоянной времени релаксации электрического заряда в металлах 10-6 с, а конкретно для меди из эксперимента [16] - 3,6·10-6 с. Поскольку измерение характеристик магнитного поля не представляет серьезной технической проблемы, следовательно, поле электрического векторного потенциала  проводника с током является реально измеряемой физической величиной.

Для иллюстрации реальности и физической значимости поля электрического вектор-потенциала  введем, аналогично вектору плотности потока ЭМ энергии Пойнтинга , потоковый вектор , который для цилиндрического проводника с током запишется в конкретном виде:

Рекомендуем скачать другие рефераты по теме: банк курсовых, бесплатные решебники скачать.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата