Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Паросочетание называется максимальным, если никакое его надмножество не является независимым.

Две вершины в графе связаны, если существует соединяющая их простая цепь.

Граф, в котором все вершины связаны, называется связным.

Граф, состоящий только из изолированных вершин, называется вполне несвязным.

Длиной маршрута называется количество ребер в нем (с повторениями).

Расстоянием между вершинами u и v называется длина кратчайшей цепи , а сама кратчайшая цепь называется геодезической.

Диаметром графа G называется длина длиннейшей геодезической.

Эксцентриситетом вершины v в связном графе G(V,E) называется максимальное расстояние от  вершины v до других вершин графа G.

Радиусом графа G называется наименьший из эксцентриситетов вершин.

Вершина v называется центральной, если ее эксцентриситет совпадает с радиусом графа.

Множество центральных вершин называется центром графа.

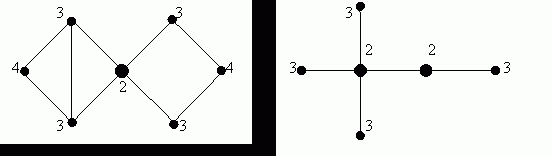
рис. 5 Эксцентриситеты вершин и центры графов (выделены).

Основные теоремы теории графов

Опираясь на приведенные выше определения теории графов, приведем формулировки и доказательства теорем, которые затем найдут свои приложения при решении задач.

Теорема 1. Удвоенная сумма степеней вершин любого графа равна  числу его ребер.

Доказательство. Пусть А1, А2, А3, ..., An — вершины данного графа, a p(A1), p(А2), ..., p(An) – степени этих вершин. Подсчитаем число ребер, сходящихся в каждой вершине, и просуммируем эти числа. Это равносильно нахождению суммы степеней всех вершин. При таком подсчете каждое ребро будет учтено дважды (оно ведь всегда соединяет две вершины).

Отсюда следует: p(A1)+p(А2)+ ... +p(An)=0,5N, или 2(p(A1)+p(А2)+ ... +p(An))=N , где N — число ребер.

Теорема 2. Число нечетных вершин любого графа четно.

Доказательство. Пусть a1, a2, a3, …, ak — это степени четных вершин графа, а b1, b2, b3, …, bm — степени нечетных вершин графа. Сумма a1+a2+a3+…+ak+b1+b2+b3+…+bm ровно в два раза превышает число ребер графа. Сумма a1+a2+a3+…+ak четная (как сумма четных чисел), тогда сумма b1+b2+b3+…+bm должна быть четной. Это возможно лишь в том случае, если m — четное, то есть четным является и число нечетных вершин графа. Что и требовалось доказать.

Эта теорема имеет немало любопытных следствий.

Следствие 1. Нечетное число знакомых в любой компании всегда четно.

Следствие 2. Число вершин многогранника, в которых сходится нечетное число ребер, четно.

Следствие 3. Число всех людей, когда-либо пожавших руку другим людям, нечетное число раз, является четным.

Теорема 3. Во всяком графе с n вершинами, где n больше или равно 2, всегда найдутся две или более вершины с одинаковыми степенями.

Рекомендуем скачать другие рефераты по теме: курсовая работа по экономике, сочинения по литературе.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата