Интеграл по комплексной переменной.

Определение 1: Кривая Г называется гладкой ,если она имеет непрерывно изменяющуюся касательную.

Определение 2: Кривая называется кусочно-гладкой ,если она состоит из конечного числа гладких дуг.

Основные свойства : Пусть на комплексной плоскости  Z задана кусочно-гладкая кривая С длиной  l, используя  параметрическое задание кривой С зададим h(t) и x (t), где h и x являются кусочно-гладкими кривыми от действительной  переменной t. Пусть a t i.

Dz i =z i – z i-1. Составим интегрируемую функцию S = åf (z*)Dz i .  (1)
где z*– производная точки этой дуги.

Если при стремлении max |Dz i |® 0 существует предел частных сумм не зависящий ни от способа разбиения кривой С на частичные дуги, ни от выбора точек z i , то этот  предел называется интегралом от функции f (z ) по кривой С.

                            (2) 

f (zi* ) = u (Pi*) + iv (Pi*)      (3)

где Dz i = Dx (t) + iDh(t)     (x (t) и h(t) - действительные числа)

Подставив (3) в (1) получим :

           (4)

Очевидно, что (4) состоит из суммы двух частных сумм, криволинейных интегралов действительной переменной. Переходя в (4) к пределу при Dx и Dh ® 0 и предполагая, что данные пределы существуют, получаем :

                                                            (5)

Заметим, что для существования криволинейного интегралов, входящих в (5), а тем самым и для существования интеграла (2) достаточно кусочной непрерывности функций u и v. Это означает, что (2) существует и в случае неаналитичности функции f (z ).

Сформулируем некоторые свойства интеграла от функции комплексной переменной. Из равенства (5) следуют свойства :

О ограниченности интеграла.

При этом z = j (z ).

   7.) Пусть Cp – окружность радиуса r, с центром в точке Z0. Обход вокруг контура Cp осуществляется против часовой стрелки. Cp : z = Z0 + r×eij,    0 £ j £ 2p,      dz = ir×eij dj .

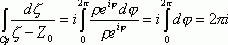
Кусочно-гладкую замкнутую кривую будем называть замкнутым контуром, а интеграл по замкнутому контуру – контурным интегралом.

Рекомендуем скачать другие рефераты по теме: семья реферат, диплом купить.





1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата