Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Очевидно, что                            (6’)

Функция (6) называется спектральной плотностью

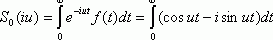
В связи с изложенным можно указать два пути отыскания спектральной плотности :

1) Вычисление интеграла (5)

2) Использование преобразования Лапласа или Фурье.

Непосредственное вычисление спектральной плотности для абсолютно интегрируемой функции.

Функция F(iu) может быть представлена, как комплексная функция действительной переменной

                                                (7)

|F(iu)| - амплитудное значение спектральной плотности, y (u) – фазовый угол.

В алгебраической форме : F(iu) = a(u) +ib(u)

                                           (8)

                                                      (9)

Для непосредственного вычисления спектральной плотности вычисляется интеграл (6), а затем по формулам (8) и (9) определяется амплитудное значение |F(iu)|  и фазовый угол y (u).

Пример.

Найти спектральную плотность импульса :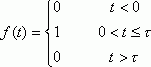

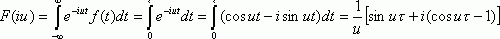
откуда , далее

Отыскание спектральной плотности для неабсолютно интегрируемых функций.

Прямое преобразование Фурье для таких функций не существует, существует преобразование Лагранжа.

Прямое преобразование Фурье необходимо :

1) Для облегчения процесса решения дифференциальных и интегральных уравнений.

2) Для исследования амплитудной и частотной характеристик спектральной плотности, определенной всюду на числовой оси.

Рекомендуем скачать другие рефераты по теме: семья реферат, диплом купить.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата