Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Сплайн-аппроксимация

Другой метод аппроксимации — сплайн-аппроксимация — отличается от полиномиальной аппроксимации Лагранжем и Ньютоном. Сплайном называется функция, которая вместе с несколькими производными непрерывна на отрезке [a, b], а на каждом частном интервале этого отрезка [xi, xi+1] в отдельности являются некоторым многочленом невысокой степени. В настоящее время применяют кубический сплайн, то есть на каждом локальном интервале функция приближается к полиному 3-го порядка. Трудности такой аппроксимации связаны с низкой степенью полинома, поэтому сплайн плохо аппроксимируется с большой первой производной. Сплайновая интерполяция напоминает лагранжевую тем, что требует только значения в узлах, но не её производных.

Метод наименьших квадратов

Предположим, что требуется заменить некоторую величину и делается n измерений, результаты которых равны xi=x+ei (i=1, 2, …, n), где ei — это ошибки (или шум) измерений, а х — истинное значение. Метод наименьших квадратов утверждает, что наилучшее приближённое значение  есть такое число, для которого минимальна сумма квадратов отклонений от :

                       

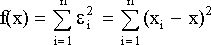
Один из наиболее общих случаев применения этого метода состоит в том, что имеющиеся n наблюдений (xi, yi) (i=1, 2, …, n) требуется приблизить многочленом степени m<n 

                        y(x)=a0+a1x+a2x2+…+amxm

Вычисленная кривая у(х) в некотором смысле даёт сложное множество значений уi. Метод наименьших квадратов утверждает, что следует выбирать многочлен, минимизирующий функцию.

                                   

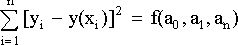
Для нахождения минимума дифференцируем  по каждой из неизвестных ak. В результате получим:

                       

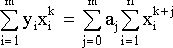
Определитель этой системы отличен от нуля и задача имеет единственное решение. Но система степеней не ортогональна, и при больших значениях n задача плохо обусловлена. Эту трудность можно обойти, используя многочлены ортогональные с заданным весом на заданной системе точек, но к этому прибегают только в задачах, связанных с особенно тщательной статической обработкой эксперимента.

Полиномы Чебышева

Критерии согласия данного метода — минимизация максимальной ошибки.

Полиномы Чебышева определяются следующим образом: Tn(x)=cos(n×arccos(x))

Например:      T0(x)=cos(0)=1,

                        T1(x)=cos(q)=x,

                        T2(x)=cos(2q)=cos2(q)-sin2(q)=2x2-1.

Можно было бы и дальше использовать тригонометрические соотношения для нахождения полиномов Чебышева любого порядка, но будет лучше установить для них рекурентное соотношение, связывающее Tn+1(x), Tn(x) и Tn-1(x):

                        Tn+1(x)=cos(nq+q)=cos(nq)cos(q)-sin(nq)sin(q),

                        Tn-1(x)=cos(nq-q)=cos(nq)cos(q)-sin(nq)sin(q).

Складывая эти неравенства, получим:

                        Tn+1(x)+Tn-1(x)=2cos(nq)cos(q)=2xTn(x);

                        Tn+1(x)=2xTn(x)-Tn-1(x).

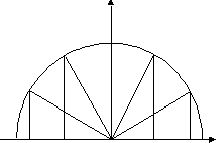
Применяя полученные формулы можно найти любой полином Чебышева. Например, Т3(x)=2xT2(x)-T1(x). Подставляя значения T2(х) и Т1(х) имеем Т3(х)=2х(2х2-1)-х=4х3-3х. Графически первые 10 полиномов Чебышева изображены ниже. Последующие полиномы по-прежнему колеблются между +1 и -1, причём период колебания уменьшаются с ростом порядка полинома.

Рекомендуем скачать другие рефераты по теме: понятие реферата, химическая реферат.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата