Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Всякая пространственно локализованная, временно устойчивая в пределах своих условных границ, форма движения материи непрерывно взаимодействует с другими соседними формами движения, а через них, так или иначе, взаимодействует и со всей остальной материей. Она является всего лишь некоторой внутренней, условно выделенной частью всего единого, огромного и чрезвычайно сложного механизма движения всей материи в целом, механизма непрерывного и вечного изменения ее внутреннего состояния по всему ее объему (пространству). Каждая временно устойчивая, временно стабильная форма движения (тело, атом, элементарная частица и т. п.), сохраняя свое некоторое внутреннее движение (то есть движение в пределах своих условных границ), в то же время непрерывно перемещается в пространстве, во всеобщем объеме самой материи. В процессе этого перемещения (это и есть то, что мы называем механическим перемещением, механическим движением) собственные условные границы любой такой формы (тела, атома, элементарной частицы и т. п.) не могут оставаться неизменными. Взаимодействуя с соседними формами, они непрерывно изменяются, изменяя тем самым условные стабильные собственные размеры и форму. В силу этого абсолютные (в указанном выше смысле) размеры тел и их форма изменяются не только в силу условности собственных границ.

Что все же дает нам основание называть собственные размеры тела абсолютными? Ведь понятие размера уже предполагает выбор некоторого эталона измерения и установления отношения между измеряемой величиной и этим эталоном.

Все дело здесь в том, что, имея свою собственную протяженность в пространстве, каждое тело, каждое пространственно устойчивое материальное образование, существуя объективно реально, уже тем самым находится в некотором отношении к протяженности всей материи в целом. Оно всегда находится в отношении части к целому. И хотя это отношение никогда не является в полном смысле абсолютно определенным и к тому же непрерывно изменяется, тем не менее, оно всегда есть и его удобно назвать для нас абсолютным, понимая определенную долю условности такой абсолютности. И эта условность часто не так уж плоха, например, уже в макромире. Кроме того, мы можем чисто теоретически принять для себя некоторый жесткий и абсолютно постоянный эталон протяженности (эталон длины) некоторой достаточно стабильной формы движения материи, которая бы условно считалась не перемещающейся в пространстве и неподверженной воздействию со стороны других форм. Такой прием абстрагирования, идеализации вполне допустим и всегда присутствовал в науке. Такая идеализация нужна нам для самого процесса познания.

Что же в принципе может быть эталоном протяженности, то есть эталоном длины? Как известно, в реальном историческом процессе развития науки таким эталоном явилось определенное твердое тело. При этом уже тогда, когда принимался такой эталон, ученые осознали, что чем точнее мы хотим использовать этот эталон, тем стабильнее должны быть внешние условия его сохранения. Но ученые, по крайней мере физики, в то время еще не представляли вполне осознанно и четко, что сам принятый эталон есть не что иное как некоторый пространственно устойчивый процесс, некоторое пространственно устойчивое движение, некоторая форма материального движения.

Ученые позаботились о том, чтобы при хранении и использовании эталона строго поддерживались определенные внешние условия. Но с позиций сегодняшнего дня удивительно то, что ученые не придали никакого значения самому пространственному перемещению эталона. Они почему-то решили, что это движение никак не влияет на эталон, а вернее, попросту игнорировали это движение.

Эталон находится на Земле. Земля вращается вокруг собственной оси и перемещается по своей орбите вокруг Солнца. Солнце тоже перемещается в своей Галактике и т. д. и т. д. Все эти формы движения неизбежно взаимодействуют друг с другом, оказывая друг на друга влияние. И этого никак принципиально не исключить.

Но наука не стоит на месте и современная физика, значительно продвинувшись в понимании сути вещей, перешла к другому эталону, который уже есть совершенно четко выраженный процесс. Это определенный электромагнитный волновой процесс, который не нужно сохранять непрерывно. Его всегда, в случае необходимости, можно воспроизвести.

Здесь можно провести такую историческую параллель, связанную с покорением огня человеком. Вначале человек как бы похитил огонь у самой природы и вынужден был его непрерывно сохранять, чтобы пользоваться им. Но потом он научился получать его сам по мере необходимости, и забота о сохранении огня отпала.

Волновой процесс как эталон длины есть определенным образом организованное движение материи. И это движение обязательно подвержено влиянию всех других движений, в которых участвует само эталонное движение. Поэтому такой эталон, воспроизводимый на Земле, или в какой-либо иной, движущейся в мировом пространстве лаборатории, не может быть абсолютным. Он изменяет свою абсолютную (в нашем понимании) длину непрерывно. Но в своей собственной системе отсчета он всегда остается эталоном со своей собственной длиной, всегда равной единице, вернее, принятой за единицу. И все измерения в системе выполняются с помощью этого эталона.

Уже здесь становится совершенно ясным, что если две какие-либо материальные системы отсчета (СО) находятся в пространстве в различном для каждой из них абсолютном движении, то они не могут быть совершенно одинаковыми. Если аналогичные СО движутся в пространстве с разными абсолютными скоростями, то они имеют и разные абсолютные размеры для всех аналогичных тел, но сохраняют при этом одни и те же внутренние пространственные отношения между внутренними телами. Причем эти отношения между аналогичными телами и процессами будут точно такими же, как и в СО, которая вся в целом не находится в абсолютном движении (то есть не находится в абсолютном механическом перемещении). Конечно же, на любую СО оказывает влияние и ее глобальное окружение, изменяя то, что мы называем гравитационным полем, и в котором СО неизбежно находится.

Полностью изолированных, замкнутых, единых и целых по отношению к самим себе и в то же время движущихся в пространстве СО в природе, как таковой, просто не существует. И если мы говорим об ИСО, то всегда должны помнить, что это некоторая идеализация материальной СО. Создавая такую идеализированную ИСО, мы считаем, что каждое из тел, находящихся в ней, существует как бы само по себе, что отдельные тела никак не влияют друг на друга, если они не сталкиваются между собой. Только электрически заряженные тела взаимодействуют на расстоянии. Но на самом деле это не так. Мы тем самым просто игнорируем объективно реальное единство мира, в основе которого лежит его материальность, то есть принадлежность всего сущего единому материальному субстрату.

Из сказанного следует, что, казалось бы, нет и не может быть внутри самой материи никакого единого абсолютного эталона длины. И действительно реально практически его нет. Но мы можем построить его для себя чисто теоретически. И это принципиально можно сделать следующим образом.

Прежде всего, свой абсолютный эталон длины мы можем представить себе в виде стоячего волнового процесса, уже принятого нами за эталон. Но этот эталон в целом не должен иметь никакого абсолютного движения (перемещения) в пространстве. Кроме того, он должен находиться при нулевом гравитационном потенциале. То есть, наш абстрактный теоретический эталон длины как бы абсолютно не подвержен никаким влияниям извне. И тогда в любой реальной точке пространства внутри материального мира мы можем представить себе рядом два эталона длины. Один из них (теоретический) всегда остается неизменным, а второй (реальный) - всегда изменяющийся в зависимости от внешних условий (гравитационного потенциала) и абсолютной скорости своего движения. С помощью первого (теоретического) эталона мы можем оценивать реальные физические изменения второго (относительного) эталона, а тем самым постигать и саму суть реальных физических изменений и взаимодействий. Другого пути для нас практически просто не существует.

Создавая свою ОТО, Эйнштейн вынужден был отказаться от абсолютного постоянства скорости света. Она по-прежнему остается постоянной лишь в СТО как некоторой идеализированной теории, рассматривающей некоторые идеализированные абстрактные СО. При рассмотрении физических систем при разных гравитационных потенциалах, причем при сугубо теоретическом их рассмотрении, оказалось, что скорость света постоянна лишь локально, как некоторое локальное отношение внутри каждой локальной СО. Свои местные эталоны длины и времени в той или иной конкретной СО мы принимаем на основе некоторого единого для всех СО правила. Это правило заключается в использовании определенных электромагнитных волновых процессов, связанных с излучением атомов. Излучение изменяется реально, но скорость света как некоторое число всегда остается постоянной. А мы узнаем о ее абсолютном изменении при разных физических условиях в разных местах пространства именно потому, что не совсем осознанно применяем к ее "измерению" как раз те теоретические абсолютные эталоны длины и времени, о которых мы только что и говорили. Правда, мы говорили пока только об эталонах длины, но то же самое относится и к эталонам времени.

То, что в своей ОТО Эйнштейн рассматривает и замедление времени в гравитационном поле, и изменение эталона длины, и изменение самой скорости света как некоторые реальные физические эффекты, и есть свидетельство того, что он сам, не осознавая этого вполне четко, становится на точку зрения рассмотрения указанных эффектов с позиций некоторой теоретической абсолютной измерительной СО с указанными нами абсолютными теоретическими эталонами. Однако он уже был близок к тому, чтобы признать это окончательно. "Но, что в общей теории относительности, - замечает он в одной из своих работ, - не существует привилегированных, однозначно связанных с метрикой пространственно-временных координат более характерно для математической формы (выделено мной - А.Ю.) этой теории, чем для ее физического содержания" (СНТ, т.2, с.158). Замечательное по своей сути признание! Эти "привилегированные, однозначно связанные с метрикой пространственно-временные координаты" и есть та теоретическая абсолютная измерительная СО, о которой мы и говорим.

Абсолютно все свойства и качества, а также состояния субстрата материи мы должны мыслить обязательно распределенными в объеме, то есть в пространстве, самого этого субстрата, так как никак иначе они принципиально существовать не могут. А различные пространственные соотношения мы изучаем с помощью геометрии. И если раньше считалось, что существует лишь одна единственная геометрия (геометрия Евклида), которую мы начинаем изучать уже в школе, то сегодня мы уже знаем, что вообще то геометрий может быть много (Римановы геометрии). И еще до сих пор в научной литературе продолжается спор, а какова же действительная геометрия нашего реального физического пространства. И зачастую эти споры ведутся не вполне корректно. Попробуем разобраться, почему же это происходит.

Все дело здесь в том, что будет принципиально правильным любую геометрию вообще рассматривать как некоторое абстрактное теоретическое построение. Оно конструируется таким образом, что способно некоторым непротиворечивым образом однозначно выразить различные пространственные отношения внутри некоторого заданного объема или на некоторой заданной поверхности. Каждая геометрия строится на основе принятия определенных аксиом и правил, а также принятия определенных "элементов конструирования", таких, например, как, что считать прямой, кривой, окружностью, лучом, углом, отрезком, равными отрезками, если они отстоят на некотором расстоянии друг от друга, параллельными отрезками и т. д. и т. п.

Как известно, наиболее простой, наглядной и привычной для нас является абстрактная геометрия Евклида. И любые пространственные отношения и соотношения в объеме субстрата материи мы принципиально можем выразить с ее помощью. А ставить вопрос о том, какова же действительная геометрия реального физического пространства вообще просто не корректно. Это все равно, что задавать вопрос о том, а какой же из существующих алфавитов, или языков действительный. Так же, как любую мысль мы можем выразить на разных языках, точно так же любые пространственные отношения и соотношения мы можем выразить с помощью разных геометрий. Геометрия - это тот же язык. Это язык измерения и выражения пространственных отношений и соотношений. И вопрос заключается лишь в том, где и как нам удобней применить тот или иной геометрический язык. Но все же наиболее простым, наглядным и удобным для нас, для нашего пространственного восприятия является язык геометрии Евклида.

Геометрия Евклида называется плоской, так как плоскость - в ней действительно плоскость, как мы привыкли ее видеть и понимать, прямая - действительно прямая, параллельные прямые - действительно параллельны между собой и т. д. Луч света мы считаем идеальным образом прямой. И успешно используем этот образ в данной геометрии. Но это всего лишь абстракция. Пройдя огромные расстояния в объеме материи, он искривляется. И если мы по-прежнему будем считать луч света образом прямой (а прямая - это один из главных конструктивных элементов любой геометрии), то уже такая глобальная геометрия не будет плоской. А то пространство, где такая геометрия применима вместе со многими другими ее конструктивными элементами, называется искривленным. Но "искривленная" геометрия не обязательно должна быть глобальной. Уже некоторая внутренняя геометрия любой сферы, где за образ "прямой" принят кратчайший отрезок, соединяющий две какие-либо отстоящие друг от друга точки на ее поверхности, тоже является "искривленной".

Изучая реально физический мир локально (причем в довольно больших пределах по нашим Земным меркам), мы успешно используем геометрию Евклида, а поэтому и говорим, что само изучаемое нами реальное физическое пространство в данных пределах евклидово. Но когда мы начинаем расширять свои физические исследования, на несколько порядков изменяя их (в мегамир), то мы должны четко осознать тот факт, что наши практические измерения возможны лишь на отличном от евклидового геометрическом языке. И мы опять же таки говорим, что само пространство при этом становится не евклидовым. Но теперь мы совершенно четко должны понимать, что же все это действительно означает. А перевести реальную картину происходящего на самый удобный и привычный для нас геометрический язык можно лишь с помощью теоретической абсолютной СО. Это все равно, что перевести какой-либо мало понятный иностранный текст на тот язык, на котором мыслишь.

Если мы хотим достичь как можно более полной ясности и наглядности в своем анализе объективно реального мира и происходящих в нем взаимодействий, то мы обязательно, в конечном счете, должны рассмотреть их с точки зрения протекания в пространстве и во времени как таковых. При этом мы должны использовать понятие "чистого" пространства, каковым является именно геометрический объем, то есть это пространство без каких-либо других примесей. Любые другие физические "примеси" к объему (пространству) усложняют анализ, так как мы вынуждены при этом рассматривать явление в его проявлении сразу по отношению к нескольким свойствам или качествам субстрата материи.

В современной литературе по физике и философии понятие "пространство" стало использоваться настолько неоднозначно, что не всегда даже ясно, что имеют в виду те или иные авторы, применяя его. Часто под этим понятием подразумевают чуть ли не все сразу свойства и качества самого субстрата материи. И это связано именно с тем, что сам субстрат материи объемен и все его свойства и качества, естественно, существуют в его объеме, то есть в его пространстве. И волей - неволей получается так, что понятие "пространство" отождествляется с самим субстратом материи. А это, конечно, усложняет сам анализ его отдельных свойств и качеств, их пространственного проявления. Все это подчеркивает настоятельную необходимость придать понятию "пространство" четкую определенность и однозначность.

По мнению автора это понятие в отношении реального физического пространства следует, прежде всего, четко связать с объемом материи, как всей сразу, так и отдельных ее частей. Однако во многих случаях не лишним будет и следующее разграничение понятия "пространство". Если нас интересуют лишь чисто геометрические отношения в объеме материи, то можно конкретизировать, что речь идет о чисто геометрическом пространстве. Если же мы имеем в виду геометрическое пространство материи (или его часть) с его внутренней "начинкой", то его можно называть физическим пространством, имея в виду ту конкретную физическую среду с ее конкретным состоянием, с которым мы имеем дело в том или ином случае.

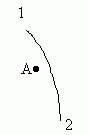
Рассмотрим такой простой пример (рис.1). В какой-то части геометрического пространства материи из точки 1 излучается световой луч, который, пройдя огромное расстояние, воспринимается затем в некоторой точке 2. При своем распространении луч проходит где-то в окрестности массивного тела А, а поэтому его траектория искривляется. Изменяется также его реальная скорость распространения вдоль кривой 1-2. Вначале она реально уменьшается при приближении к телу А, а затем реально возрастает при удалении от тела А.

Рекомендуем скачать другие рефераты по теме: курсовики скачать бесплатно, реферат г.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата