Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

г) d(Хi, Хj) £ d(Хi, Хk) + d(Хk, Хj), где Хj; Хi и Хk - любые три вектора из Ер.

Значение d(Хi, Хj) для Хi и Хj называется расстоянием между Хi и Хj и эквивалентно расстоянию между Gi и Gj соответственно выбранным характеристикам (F1, F2, F3, ..., Fр).

Наиболее часто употребляются следующие функции расстояний:

1. Евклидово расстояние         d2(Хi , Хj) =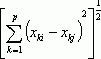

2. l1 - норма                                          d1(Хi , Хj) =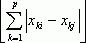

3. Сюпремум - норма              d¥ (Хi , Хj) = sup

k = 1, 2, ..., р

4. lp - норма                              dр(Хi , Хj) =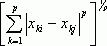

Евклидова метрика является наиболее популярной. Метрика l1 наиболее легкая для вычислений. Сюпремум-норма легко считается и включает в себя процедуру упорядочения, а lp - норма охватывает функции расстояний 1, 2, 3,.

Пусть n измерений Х1, Х2,..., Хn представлены в виде матрицы данных размером p ´ n:

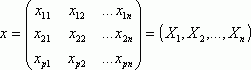
Тогда расстояние между парами векторов d(Хi , Хj) могут быть представлены в виде симметричной матрицы расстояний:

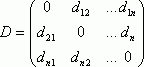
Понятием, противоположным расстоянию, является понятие сходства между объектами Gi. и Gj. Неотрицательная вещественная функция S(Хi ; Хj) = Sij  называется мерой сходства, если :

1) 0£ S(Хi , Хj) djk

B(w) =, если dik £ djk

B(w) = , если dik >  djk

где ni  и nj - число элементов в кластерах i и j, а w – свободный параметр, выбор которого определяет конкретный алгоритм. Например, при w = 1 мы получаем, так называемый, алгоритм «средней связи», для которого формула перерасчета расстояний принимает вид:

di+j,k =

В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным среднему арифметическому из расстояний между всеми такими парами элементов, что один элемент пары принадлежит  к одному кластеру, другой - к другому.

Наглядный смысл параметра w становится понятным, если положить w ® ¥. Формула пересчета расстояний принимает вид:

di+j,k = min (di,k djk)

Это будет  так называемый алгоритм «ближайшего соседа», позволяющий выделять кластеры сколь угодно сложной формы при условии, что различные части таких кластеров соединены цепочками близких друг к другу элементов. В данном случае расстояние между двумя кластерами на каждом шаге работы алгоритма оказывается равным расстоянию между двумя самыми близкими элементами, принадлежащими к этим двум кластерам.

Довольно часто предполагают, что первоначальные расстояния (различия) между группируемыми элементами  заданы. В некоторых  задачах это действительно так. Однако, задаются только объекты и их характеристики и матрицу расстояний строят исходя из этих данных. В зависимости от того, вычисляются ли расстояния между объектами или между характеристиками объектов, используются разные способы.

В случае кластер анализа объектов наиболее часто мерой различия служит либо квадрат евклидова расстояния

Рекомендуем скачать другие рефераты по теме: растения реферат, диплом государственного образца.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата