Министерство общего и профессионального образования РФ

Гимназия № 12

реферат

на тему:  Комплеклсные числа

                                                                                        Выполнил:          ученик 9 “Д”                   класса

                                                                                                                    Крутько Е.А.

                                                                                        Проверила:  Санина В.Г.

Тюмень 1999

План.

1. Зачем нужны новые числа?

2. Неприводимый случай кубического уравнения.

3. Действительное + мнимое = комплексное.

      

       Когда мы слышим слово “число”, то на ум прежде всего приходят натуральные числа: 1, 2, 3… Их мы используем для пересчета разнообразных предметов. Если натуральных чисел оказывается недостаточно, прибегаем к дробям, а точнее – к рациональным числам. И то, как правило, не ко всем, а лишь к тем, которые выражаются конечными десятичными дробями. Уж их-то вполне хватает для повседневных нужд. Конечные десятичные дроби позволяют фиксировать результаты всевозможных измерений с произвольной точностью. Чего же еще ждать от чисел?

       Но вот нам говорят, что существуют несоизмеримые величины. Например, диагональ квадрата несоизмерима с его стороной, т.е. отношение их длин -- не является рациональным числом, хотя и может с любой наперед заданной точностью быть приближенно рациональным числом. И тогда становится понятно, что проще признать эти новые, иррациональные числа, чем каждый раз вместо “решим уравнение x2=2 ”говорить“ найдем такое x, чтобы x2 отличалось от 2 не более, чем на такую-то величину”.

       Построенное таким образом сообщество – множество действительных чисел – уже не только удовлетворяет нашим практическим потребностям, но и обладает определенной теоретической полнотой. Оно позволяет формулировать разнообразные задачи, сводить их к уравнениям и решать, не боясь впасть в противоречие. Нельзя, например, делить на нуль, нельзя извлекать корень четной степени из отрицательных чисел и т.д. Однако правила эти несложны, и если им строго следовать, то все будет в порядке…

       Но все ли? Рассмотрим такой пример:  можно считать равным и 1, и –1, а определить  невозможно. С другой стороны, что такое 1/6? Это то же самое, что 2/12. Однако = (-1)1/6, (-1)2/12 , а последний корень можно извлечь!

       Вот еще один пример: .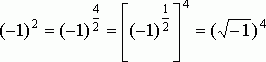

Но если квадратного корня из –1 не существует, то и его четвертой степени не существует. Значит, -1 нельзя возвести даже в квадрат?

       Кому-то покажется, что все это не настоящие противоречия. Можно наложить дополнительные запреты на действия с числами, и подобные ситуации больше не возникнут. Но всегда ли разумны запреты? Представьте себе, что некоторые задачи весьма успешно решаются только с нарушением определенного запрета, и никак не удается найти “законного” способа их решения. Не стоит ли в таком случае отказаться от ограничения, ставшего слишком обременительным? Именно это произошло в свое время с запретом извлекать квадратный корень из отрицательных величин при решении так называемого неприводимого случая кубического уравнения.

Для решения уравнения вида   была выведена формула

,

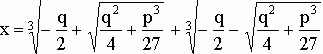прдобно тому как для решения квадратного уравнения существует общая формула, выражающая корни уравнения через его коэффиценты, аналогичная формула есть и для кубического уравнения. Она называется формулой Кардано – по имени математика, впервые ее опубликовавшего. Но, к примеру, для уравнения

х3 = 30х + 36

Формула Кардано дает

х =

Рекомендуем скачать другие рефераты по теме: грибы реферат, чужие сообщения.





1  2 | Следующая страница реферата