Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

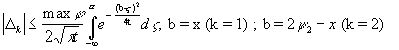; (7)

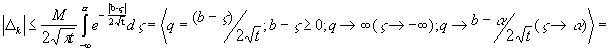
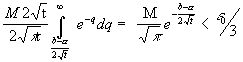, (7.1)

b=x ( k=1 ) , b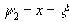=2(k=2) 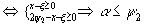оценка (7.1) эквивалентна системе неравенств:

,

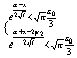откуда:

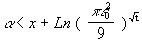. (8)

Т. к. в работе исследуется поведение неравенства (3) при 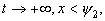то принимаем что для некоторого :

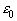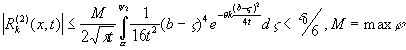. (9)

3. Формулировка результата в виде теоремы

Обобщая результаты всей работы в целом можно сформулировать следующие теоремы:

1. Пусть для уравнения теплопроводности имеет место задача

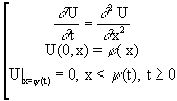(З)

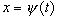- гладкая, непрерывно - дифференцируемая функция на 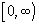,а функция 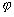ограничена на R : .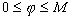

Тогда для любого сколь малого числа 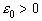можно указать число

,

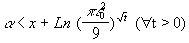такое что имеет место следующая оценка “сверху” решения задачи (З):

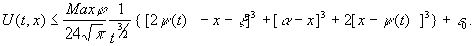
Раскрыв квадратные скобки, получим:

.

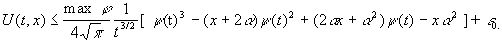2.Пусть в имеет место задача (З), 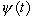- монотонная, неограниченная, возрастающая функция,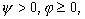

тогда:

если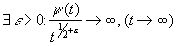 , то

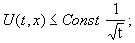
2) если 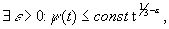то

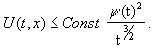
Замечанние:видно, что оценку полученную в теореме 2 можно получить и при более слабых ограничениях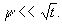

4. Примеры

Пусть ,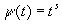

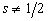
Рекомендуем скачать другие рефераты по теме: жизнь человека реферат, объект реферата.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата