Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

при росте объемов выборок приближается к стандартному нормальному распределению (с математическим ожиданием 0 и дисперсией 1).

  Правила принятия решений и таблица критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (2). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?

  Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (1) статистика T будет асимптотически нормальна с параметрами

E(T) =  ( 12mn ) 1/2 (1/2 - a) (m+n+1) - 1/2  ,

D(T) = 12 [(n - 1) b2  + (m - 1) g2  + a(1 -a) ] (m+n+1) - 1    .  (5)

  Из формул (5) видно большое значение гипотезы

H01:       a =  P(X < Y) = 1/2   .   (6)

Если эта гипотеза неверна, то, поскольку m # n, справедлива оценка

 u E(T) u  $ ( 12m n (2n+1) - 1) 1/2 u 1/2 - au  ,

а потому  u E(T) u безгранично растет при росте объемов выборок. В то же время, поскольку

b2 #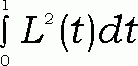 # 1, g2 #  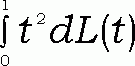# 1, a(1 -a)#1/4,

то

D(T) # 12 [(n - 1) + (m - 1) + 1/4] (m+n+1) - 1 # 12.  (7)

Следовательно, вероятность отклонения гипотезы H01 , когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (6), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе

АH01:       a =  P(X < Y) ё 1/2   .   (8) .

  Если же гипотеза (6) верна, то статистика T асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой

D(T) = 12 [(n - 1) b2  + (m - 1) g2  + 1/4 ] (m+n+1) - 1    .  (9)

Гипотеза (6) является сложной, дисперсия (9), как показывают приводимые ниже примеры, в зависимости от значений b2 и g2 может быть как больше 1, так и меньше 1, но согласно неравенству (7) никогда не превосходит 12.

  Приведем пример двух функций распределения F(x) и G(x) таких, что гипотеза (6) выполнена, а гипотеза (2) - нет. Поскольку

a =  P(X < Y) =  òF(x)dG(x) ,  1 - a =  P(Y < X) =  òG(x)dF(x) (10) ,

и  a = 1/2 в случае справедливости гипотезы (2), то для выполнения условия (6) необходимо и достаточно, чтобы

ò(F(x) - G(x)) dF(x) = 0  (11) ,

а потому естественно в качестве F(x) рассмотреть функцию равномерного распределения на интервале (-1 ; 1). Тогда формула (11) переходит в условие

ò(F(x) - G(x)) dF(x) = - 1/2 ò(G(x) - (x + 1)/2 ) dx = 0  (11) .

Это условие выполняется, если функция  (G(x) - (x + 1)/2 ) является нечетной.

Рекомендуем скачать другие рефераты по теме: шпаргалки по психологии, оформление доклада.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата