Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

rn0 - р = 0, (2.6)

где r - радиус-вектор произвольной точки M(x, y) этой прямой, n0 - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.

Нормальное уравнение прямой в координатной форме имеет вид:

x cosα + y sinα - р = 0,

где α - величина угла, образованного прямой с осью Оx.

Уравнение пучка прямых с центром в точке А(x1, y1) имеет вид:

y-y1 = λ(x-x1),

где λ - параметр пучка.

Если пучок задается двумя пересекающимися прямыми A1x + B1y + C1= 0,
A2x + B2y + C2 = 0, то его уравнение имеет вид:

λ(A1x + B1y + C1) + μ(A2x + B12y + C2 )=0,

где λ и μ - параметры пучка, не обращающиеся в 0 одновременно.

Величина угла между прямыми y = kx + b и y = k1x + b1 задается формулой:

tgφ = .

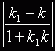Равенство 1 + k1k = 0 есть необходимое и достаточное условие перпендикулярности прямых.

Для того, чтобы два уравнения

A1x + B1y + C1= 0, (2.7)

A2x + B2y + C2 = 0, (2.8)

задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:

A1/A2 = B1/B2 = C1/C2.

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если A1/A2 = B1/B2 и B1/B2 ≠ C1/C2; прямые пересекаются, если A1/A2 ≠ B1/B2 .

Расстояние d от точки M0(x0, y0) до прямой есть длина перпендикуляра, проведенного из точки Mо к прямой. Если прямая задана нормальным уравнением, то d = |r0 n0 - р| , где r0 - радиус-вектор точки M0 или, в координатной форме, d = |x0cosα + y0sinα - р|.

Общее уравнение кривой второго порядка имеет вид:

a11x2 + 2a12xy + a22y2 + 2a1x +2a2y +a = 0.

Предполагается, что среди коэффициентов a11, a12, a22 есть отличные от нуля.

Уравнение окружности с центром в точке С(a, b) и радиусом, равным R:

Рекомендуем скачать другие рефераты по теме: шпоры по математике, реферат по технологии.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата