Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

 

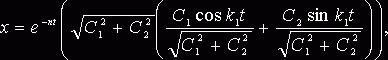
положим, что

  ,

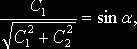
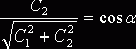тогда

                                                     (5)

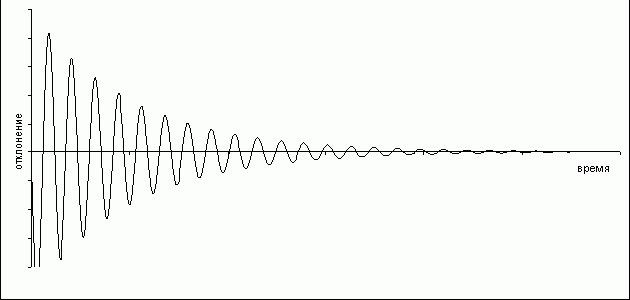
График зависимости отклонения от положения равновесия от времени имеет вид:

Если заданы начальные условия:  при t = 0, то можно определить А и a. Для этого находим

и   подставляем  t = 0  в  выражения   для и  получим систему уравнений

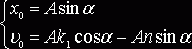
Разделелив обе части второго уравнения на соответствующие части первого получим

 

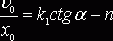
откуда

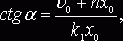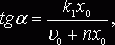    или   а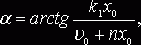     

Так как

 

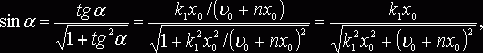
то

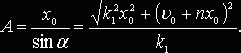
Решение (5) показывает, что имеют место затухающие колебания. Действии-тельно, амплитуда колебания  зависит от времени и является монотонно убывающей функцией, причем  при .

Период затухающих колебаний определяется по формуле

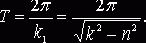
Моменты времени, в которые груз получает максимальное отклонение от начала координат (положения равновесия), образуют арифметическую прогрессию с разностью, равной полупериоду Т/2. Амплитуды затухающих колебаний образуют убывающую геометрическую прогрессию со знаменателем, равным  или . Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.

Частота колебаний в этом случае меньше, нежели в предыдущем (), но, как и там, не зависит от начального положения груза.

Если сопротивление среды велико и , то, положив , получим корни (4) в виде  Так как , то оба корня отрицательны. Общее решение уравнения в этом случае имеет вид

Рекомендуем скачать другие рефераты по теме: конспект занятия, реферати українською.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата