Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Температурный сдвиг не изменяет вид спектра поглощения (1.10), а лишь дает вклад в его смещение относительно нуля скоростей (или эталонного поглотителя).

Изомерный (химический) сдвиг мессбауэровского спектра. Его природа обусловлена электростатическим взаимодействием ядра с окружающим электронным зарядом (электрическое монопольное взаимодействие).

Изомерный сдвиг спектральной линии поглощения относительно линии излучения определяется выражением [7, 12]

 (1.12)

и представляет собой произведение двух сомножителей. Первый из них содержит лишь ядерные параметры: заряд ядра  и среднеквадратичные радиусы ядра ,  в основном и возбужденном состояниях, а второй – атомные: плотности  электронного заряда в точке расположения ядра (r=0) в поглотителе (а) и источнике (s). Для изотопа Fe среднеквадратичный радиус ядра в основном состоянии больше, чем в возбужденном. Поэтому изомерный сдвиг  при увеличении плотности заряда на ядре в поглотителе уменьшается, а при её уменьшении – увеличивается.

Сдвиг несет информацию о перераспределении внешних s- и d-электронов резонансного атома. Электронную плотность на ядре создают только электроны s-симметрии со сферическими волновыми функциями; d-электроны (так же, как p- и f-) имеют «узел» (т.е. нулевую плотность) на ядре, но влияют на изомерный сдвиг косвенно, экранируя s-электроны. При увеличении числа d-электронов изомерный сдвиг Fe увеличивается, и наоборот.

Для сплавов и соединений железа влияние p-электронов значительно слабее, чем d-электронов и часто не учитывается.

Формула (1.12) задаёт изомерный сдвиг поглотителя относительно резонансного изотопа в матрице источника. При сравнении изомерных сдвигов одного и того же изотопа в различных сплавах и химических соединениях величина этих сдвигов должна быть выражена относительно некоторого единого эталона. Для сплавов железа эталоном обычно служит α-Fe. Сдвиг относительно эталона легко определить, если известны сдвиги для эталона и исследуемого вещества относительно какого-либо источника.

Вследствие то, что внутренние s-оболочки не претерпевают существенных изменений при образовании твердых растворов и химических соединений, изомерный сдвиг Fe несет информацию о перераспределении внешних s- и d-электронов. Вследствие этого его называют также химическим сдвигом. Изменение химического сдвига в ряду соединений или сплавов дает непосредственную информацию о характере изменения химической связи.

Изомерный сдвиг приводит к смещению «центра тяжести» мессбауэровского спектра, задаваемого соотношением (1.10), относительно эталонного поглотителя.

Отметим, что интерпретация изомерных сдвигов для сплавов переходных металлов встречает значительные трудности в связи с отсутствием для них строгой электронной теории.

Квадрупольное расщепление . Ядра со спином 0 и 1/2 имеют сферически-симметричную форму. Их электрический квадрупольный момент вследствие этого равен нулю. Ядра со спином I > 1/2 не обладают сферической симметрией и характеризуются квадрупольным моментом Q, отличным от нуля. Взаимодействие квадрупольного момента с градиентом электрического поля (создаваемым окружающими электрическими зарядами) приводит к частичному снятию вырождения по магнитному квантовому числу и расщеплению уровней ядра на подуровни (появляется зависимость энергии от квадрата магнитного квантового числа ). Величина расщепления возбужденного уровня ядра Fe со спином I = 3/2, находящегося в поле с аксиально симметричным градиентом электрического поля , определяется выражением [7.12] (см. рис. 1.3б)

, (1.13)

где  – фактор антиэкранирования, позволяющий учесть влияние частично заполненных оболочек мессбауэровского атома на градиент электрического поля. Этот градиент, обусловленный окружающими мессбауэровский атом зарядами ионов, не равен нулю, если симметрия окружения резонансного атома ниже кубической. В приближении точечных зарядов компоненты тензора градиента могут быть найдены из выражения [7].

, (1.14)

где n – единичный вектор в направлении ;  – символ Кронкера.

При значительном расщеплении вектора ( >> Г) спектр поглощения представляет собой хорошо разрешенный дублет (см. рис. 1.3б). Поскольку градиент электрического поля снижается с увеличением расстояния пропорционально 1/R³, наибольшее влияние на его величину оказывают атомы ближайшего окружения. В твердых растворах, например, значительное квадрупольное расщепление резонансного уровня возникает в том случае, когда в ближайшем окружении мессбауэровского атома появляется примесь внедрения. Теоретическая форма дуплета может быть представлена суперпозицией двух лоренцевских линий:

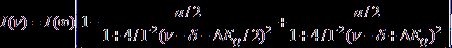. (1.14)

Как и в случае изомерного сдвига,  определяется произведением ядерного и атомного сомножителей. Величина Q резонансного ядра является ядерной константой, её находят из независимых экспериментов. Значения Q для ядер различных изотопов приведены, например, в монографии В. С. Шпинеля [12]. Атомный множитель  может быть рассчитан теоретически. Сравнивая его величину с расстоянием между линиями экспериментального дублета, можно идентифицировать положение атомов в решетке твердого раствора. Из сравнения эксперимента с результатами расчетов, например, в модели точечных зарядов, может быть оценено зарядовое состояние примеси в кристалле.

Магнитное дипольное расщепление. Если атомное ядро в энергетическом состоянии E, обладающее отличным от нуля магнитным моментом μ, поместить постоянное во времени магнитное поле Н, то энергия ядерного состояния изменится на величину [13]

∆E = - (μН)= - ()μН, (1.16)

где I – спин ядра в состоянии с энергией E,  – магнитное квантовое число, принимающее 2I + 1значений: I, I – 1, …, -I. Поскольку, в отличие от случая электрического квадрупольного взаимодействия, изменение энергии ∆E пропорционально первой степени , вырождение по магнитному квантовому числу снимается полностью. В отсутствие магнитного поля в экспериментах по ядерному гамма-резонансу измеряются переходы между состояниями ,  и , , а при наличии поля между , ,  и , , . Правила отбора для магнитного квантового числа , приводят для ядра Fe (= 0, = 1/2, = ±1/2 и = 14,4 кэВ, = 3/2, = ±1/2, ±3/2) к шести разрешенным переходам и к взаимодействию в мессбауэровских спектрах магнитоупорядоченных веществ шести отдельных линий поглощения (ядерный эффект Зеемана) (см. рис. 1.3в).

Используя значение μ(Fe) = 0,0903 ± 0,0007 я. м., полученное в работе [14] с помощью метода ЯМР, и измеренное с помощью эффекта Мессбауэра значение μ(Fe) = 0,153 ± 0,004 я. м., Ханна и др. [15] определили величину поля на ядре Fe в чистом железе при комнатной температуре: H (Fe) = 333 ± 10 кЭ.

Интенсивности линий зеемановского секстета магнитоупорядоченных веществ, содержащих мессбауэровский изотоп Fe, относятся, в случае тонкого поглотителя, как 3 : z : 1 : 1 : z : 3, где 0 ≤ z ≤ 4. Параметр z характеризует относительную интенсивность переходов 3/2 à ±1/2 (для 2-й и 5-й линий секстета) и является функцией угла между направлением пучка γ-квантов и осью магнитного поля. Для поликристаллических образцов, при условии равной вероятности различных направлений намагниченности в магнитных доменах или изотропности фактора Дебая-Валлера, среднее значение < z> = 2 [6].

Магнитное поле на ядре Fe в чистом железе антипараллельно магнитному моменту атома. Это связано с тем, что основной вклад в эффективное поле дает обменная поляризация s-электронов внутренних оболочек атома результирующим спином 3d-электронов [13]. Обменное взаимодействие s- и d-электронов обуславливает их притяжение при параллельной ориентации спинов и отталкивание при антипараллельной, что приводит к появлению отличной от нуля спиновой плотности s-электронов на ядре атома. Величина этого вклада дается выражением [7]

Рекомендуем скачать другие рефераты по теме: правила реферата, bestreferat.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата